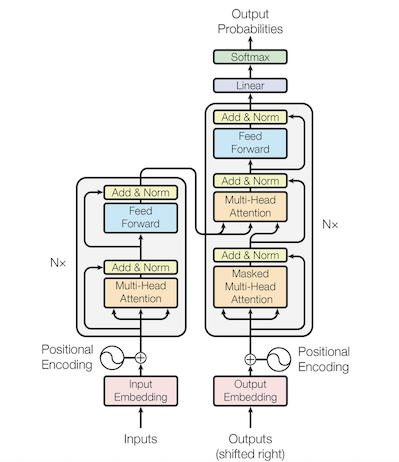
原论文链接:Attention Is All You Need
1 背景
在机器转录和语言建模上,RNN和CNN都有着广泛的应用。在RNN中,输入是按照顺序一个个输入进网络进行计算,encoder每个节点计算得到hidden state作为下一时刻的输入,decoder也是如此,一个词一个词往外蹦,但是这种模型无法进行并行化计算,并且当序列比较长的时候,会带来内存限制问题,并且由于长序列梯度消失问题,有可能会导致早些时候的输入影响力变弱,也就是说RNN可能无法看到全局的状态,尽管LSTM是这个问题的解决办法,但是这个问题并没有完全消除。在CNN中,尽管允许并行计算,但是让两个相距较远的元素产生关联,可能需要好几层卷积。
作者运用注意力机制attention解决了这一问题,提出了Transformer模型在机器翻译任务上有很好的效果。attention机制对依赖性进行建模,却可以不考虑序列中元素的距离。RNN是一个元素一个元素输入到网络中,但是transformer是将所有元素一起输入到网络中去。
2 模块讲解
2.1 Scaled dot-Product Attention
缩放点积模型见下图
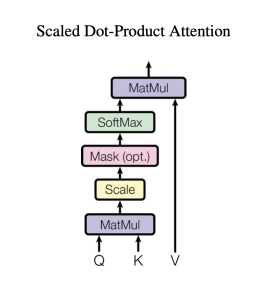
计算公式如下
\[\mathrm{Attention}(Q,K,V)=\mathrm{softmax}(\frac{QK^T}{\sqrt{d_k}})V\]
在本小节中,我们假设有n个query,m对key-value pair,query、key维度为\(d_k\),value的维度为\(d_v\)。Query,Key, Value是什么,请见之前的文章注意力机制。首先Q与K进行矩阵乘法,其实就是每个query和所有的key做内积(内积可以反应两个向量的相似度,内积越大,两个向量越相似)得到矩阵B,矩阵B中每一个蓝线是一个query对所有key的内积值,然后对每一行做softmax,得到矩阵A,矩阵A每一行的加和就为1(每一行可以看成由其对应的query得到的注意力分布\(\alpha_n\),相当于一个权重)。最后,矩阵A再和Value相乘,得到输出矩阵,输出矩阵每一个红线就是所有value按照某个query得到的注意力分布加权求和得到,比如说输出矩阵的第i行就是所有value按照矩阵A第i行(由于已经softmax过,故加和为1)的值加权求和得到。下面两幅图中,上图为计算过程,下图为计算示意图。
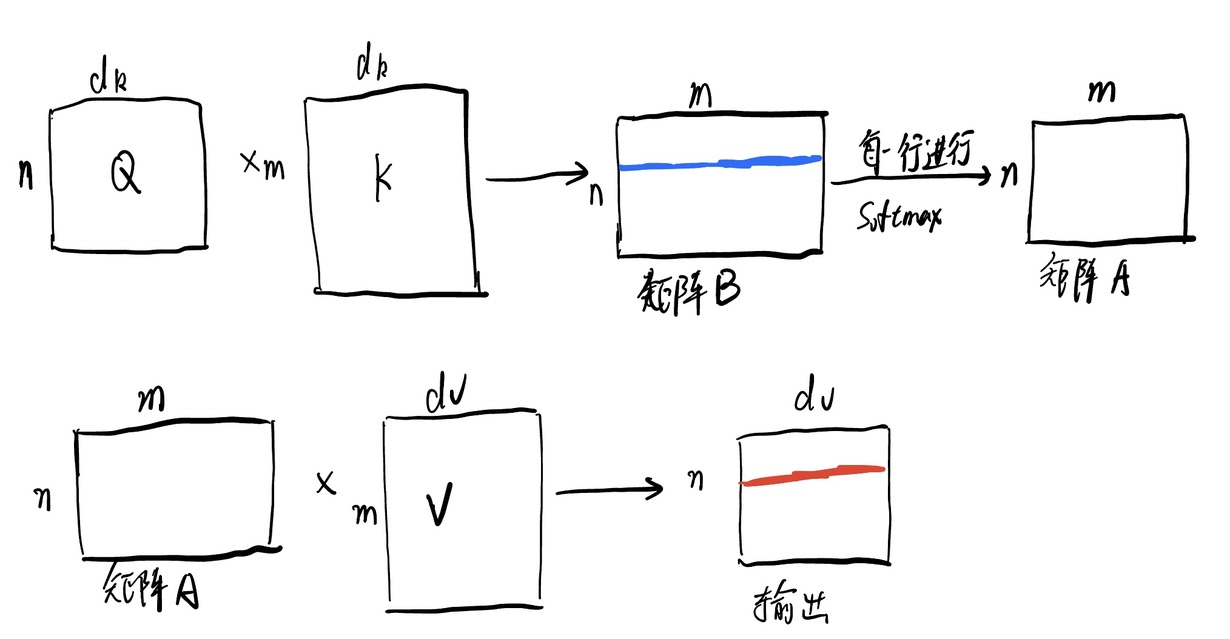
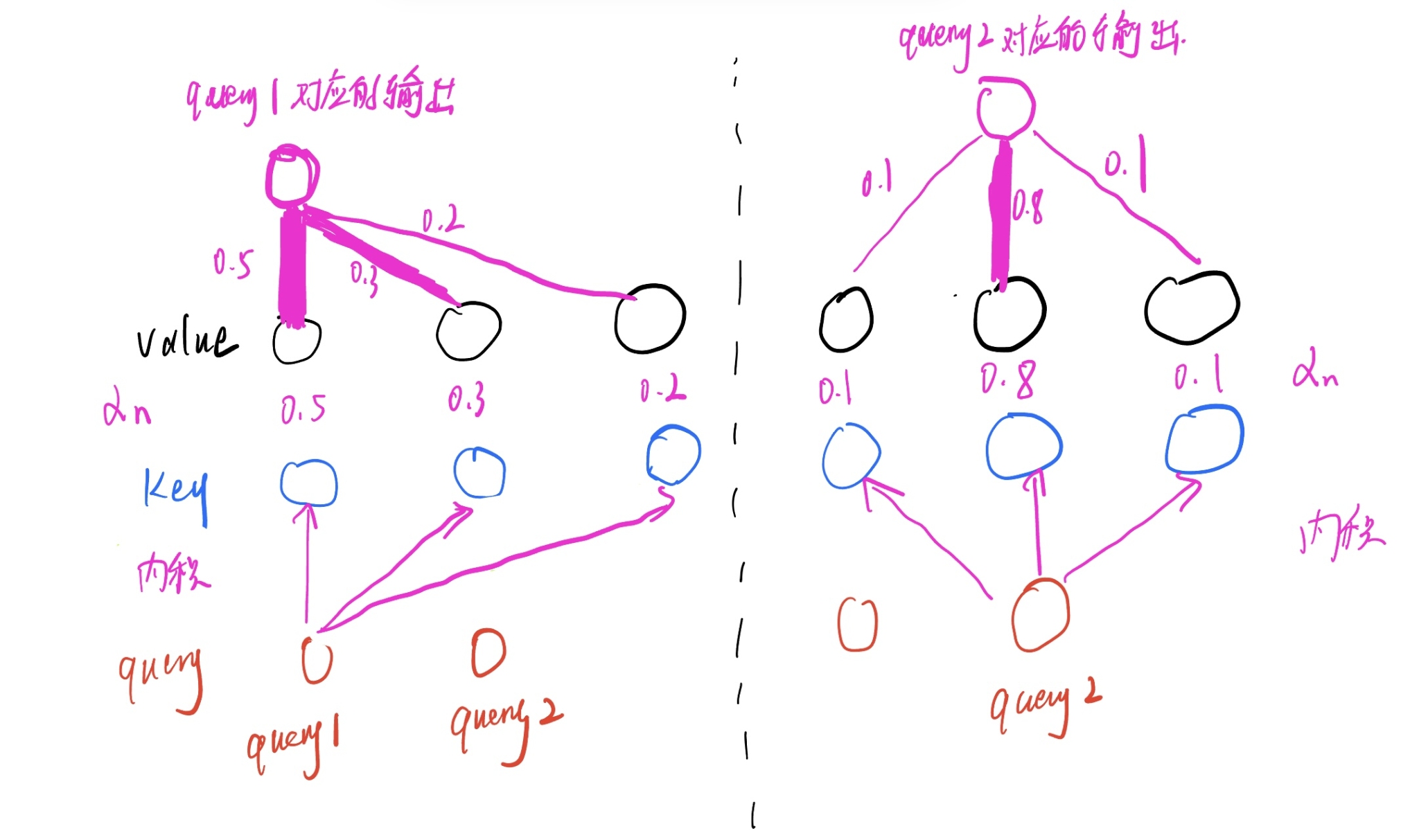
2.2 multi-head attention
2.2.1 为什么要做multi-head attention?
因为scaled Dot-product attention其实没有学习的参数,因为就只有一个内积计算,但是我们要有网络学习的内容,于是作者就构建了multi-head模型。为了学习不一样的模式,需要一些不一样的计算相似度的办法。我们投影到低维,投影的w是可以学的,也就是说给你h次机会学习到不同的投影方法,使得在投影的度量空间里,能够匹配不同模式它需要的相似函数,有一种在卷积网络里多输出通道的感觉。
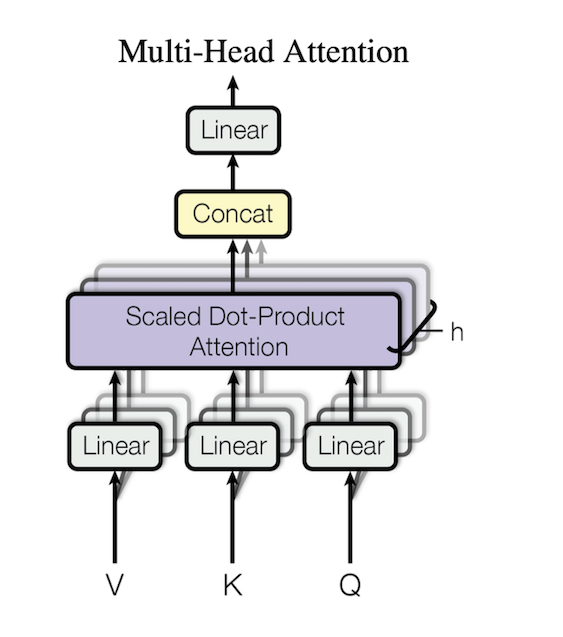
2.2.2 计算过程
- 输入:Query、Key、Value
- 输出:Value的个数✖️\(d_{\mathrm{model}}\)
将Q、K、V分别投影到一个空间上,投影h次,然后分别输入到h个Scaled Dot-Product Attention中,将输出进行concat,再经过一个线性层得到计算结果
\[\begin{aligned}\mathrm{MultiHead}(Q,K,V)&=\mathrm{Concat}(\mathrm{head}_1,…,\mathrm{head}_\mathrm{h})W^O\\\mathrm{where~head}_\mathrm{i}&=\mathrm{Attention}(QW_i^Q,KW_i^K,VW_i^V)\end{aligned}\]
\[\begin{aligned}&\text{Where the projections are parameter matrices }W_i^Q\in\mathbb{R}^{d_{\mathrm{model}}\times d_k},W_i^K\in\mathbb{R}^{d_{\mathrm{model}}\times d_k},W_i^V\in\mathbb{R}^{d_{\mathrm{model}}\times d_v}\\&\mathrm{and~}W^O\in\mathbb{R}^{hd_v\times d_{\mathrm{model}}}.\end{aligned}\]
在原论文中作者设h=8,\(\begin{aligned}d_k=d_v=d_{\mathrm{model}}/h=64\end{aligned}\)
2.3 masked multi-head-attention
为什么要做mask操作?,在推理过程中,我们在推理第t个单词时,只知道第t个单词即t之前的信息,但不知道t+1及其之后的信息,为了保证训练和推理时的一致性,加入mask操作,那为什么mask操作能保证训练和推理操作的一致性呢?
训练过程中,假设label为 <S>, <I> , <love> <you>(S为起始标签),query和key矩阵运算之后,会得到如下的矩阵,当计算的是”I”时,应该看不到love和you,当计算的是love的时候,应该看不到you,以此类推,因为我们在计算之后要输入softmax层,我们只需要把红色框标注的位置设为无穷小,便会使其失去作用(经过softmax计算后会趋近于0),这样就模拟了推理时的情况

2.4 Position-wise Feed-Forward Network
其实
把mlp作用在每一个词(position)上,每个词用共用一个MLP,假如我们有n个query,那么我们就会有n✖️\(d_{\mathrm{model}}\)的输出,我们输出中的每一行都做Feed-Forward
\[\mathrm{FFN}(x)=\max(0,xW_1+b_1)W_2+b_2\]
输入和输出都是一个1✖️\(d_{\mathrm{model}}\)的向量,内层的维数是2048,也就是说:512->2048->512
2.5 Positional Encoding
加入顺序信息,如果不加这层,任何两个含有相同单词但单词顺序不同的句子,由于QKV和顺序是无关的,经过attention层之后,尽管顺序不一样,他们的输出是一样的(输出其实就是value的加权和),这显然是不正确的。Positionnal encoding产生的向量和embedding层的维度一样,把positional encoding和embedding层相加,这样embedding就含有了顺序(时序)信息了。具体计算方法见原论文,这里不再阐述。
3 模型整体架构
transformer整体架构也可以看成encoder-decoder架构,encoder和decoder均由N个相同的layer堆叠而成,decoder在inference时是自回归的。N个layer是串联的关系,最终在第n个encoder layer得到encoder的输出
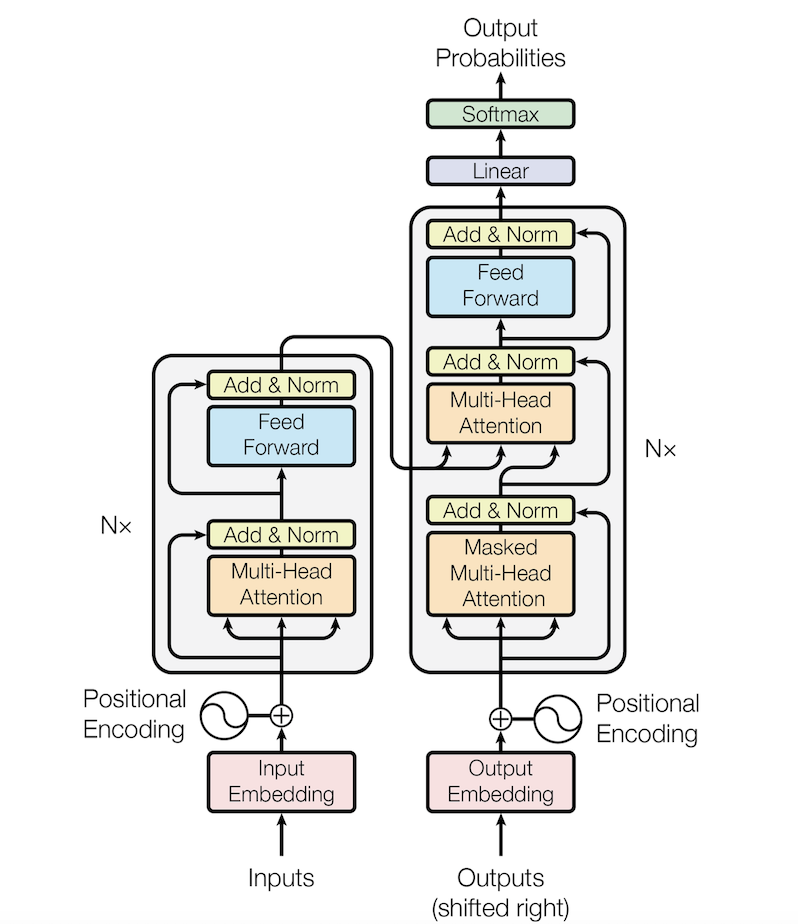
4 Train and Inference(推理和训练)
以中译英为例,我爱你->I love you
4.1 train
首先要明确,以I love you为例,在数据集中,lable是<S>, <I> , <love> <you>;target是<I> , <love> <you> <E>,其中<S>, <E>分别为开始、结束标识符。
在训练过程中,encoder的输入应该是“我爱你”,输入到encoder中去,经过n层计算,在第n层得到输出(将来会复制两份作为key和value送进decoder中)
至于decoder,输入的是<S>, <I> , <love> <you>对应的词向量,经过masked-multi-head-attention后,得到4✖️\(d_{\mathrm{model}}\)的矩阵,这个矩阵会作为query,encoder的输出会作为key,value,送进multi-head-attention层中去,再经过feed forward,重复N次,最终得到4✖️\(d_{\mathrm{model}}\)的prediction来和<I> , <love> <you> <E>对应的词向量这一target计算loss,然后反向传播更新参数。
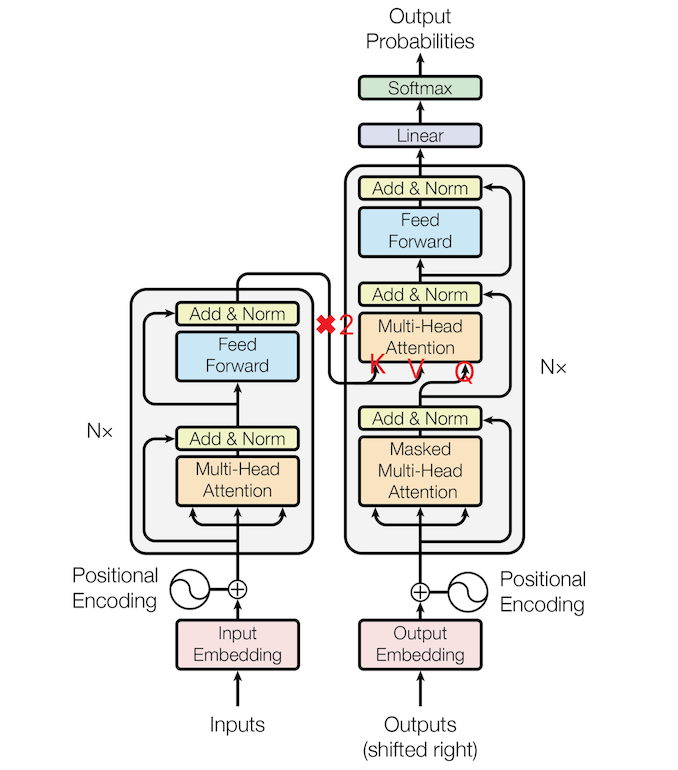
4.2 Inference
在推理过程中,encoder和train里的逻辑一样,encoder的输入应该是“我爱你”,输入到encoder中去,经过n层计算,在第n层得到输出(将来会复制两份作为key和value送进decoder中)
decoder和train里的逻辑很不一样,在推理阶段,decoder是自回归的,首先输入的是<S>对应的词向量,1✖️\(d_{\mathrm{model}}\),经N层计算,会得到一个1✖️\(d_{\mathrm{model}}\)的输出,如果推理正确,那么这个向量经过线性层,softmax分类之后,应该是单词”I”。然后我们把刚刚计算得到的单词I对应的向量输入进网络,得到1✖️\(d_{\mathrm{model}}\)向量,如果推理正确,那么该向量应该是单词”love”,以此类推,如果全部推理正确,最终得到输出是<I> , <love> <you> <E>对应的词向量。至此,推理结束。值得注意的是,我们在每层decoder layer里,都会用到encoder的输出,来作为decoder layer里multi-head-attention的key与value。
简单来说,推理时,decoder的输入就是一个query,结合encoder给的key-value,来查询它下一个词是什么。
5 思考
transformer是如何体现全局信息的呢?
在encoder层里,我们的输入是整个句子,而不是像rnn一样将单词一个个输入进去,假设句子有n个单词,我们会产生一个n✖️\(d_{\mathrm{model}}\)的向量来表示整个句子,每一行可以看成该单词在结合全文语境情况下产生的编码(因为是由所有value加权产生的),不像rnn,某一隐藏状态只有它及其之前的语境信息。且不会存在rnn中长序列梯度消失的问题。
在decoder层中,推理时,我们向decoder输入一个词,因为在multi-head-attention层中的key-value是encoder的输出,这个输出是带有全局信息的,也就是说,我们在计算当前单词的下一个单词是什么的时候,是有上下文语境的,这就大大提升了transformer的准确率。