1 No Free Lunch Theorem
“没有午餐定理”(简称NFL定理),意思就是,一个任务的分布\(f\)是均匀分布,那么对于任何两个机器学习算法\(\mathfrak{L}_{a}\)与\(\mathfrak{L}_{b}\),无论\(\mathfrak{L}_{a}\)多么聪明,\(\mathfrak{L}_{b}\)多么笨,他们的期望性能是一样的(证明请见西瓜书Page8),既然所有学习算法的期望性能都跟随机胡猜差不多,那我们还学习机器学习干嘛?
我们要注意,NFL定理的一个重要前提是,所有问题出现的机会相同,或所有问题同等重要,任务的分布是均匀分布,但是很多时候,我们是想为我们试图解决的问题(例如某个具体应用任务)找一个方案,至于这个方案在其他任务上,甚至是相似的任务上是否有效,我们是不关注的。
事实上,上面 NFL 定理的简短论述过程中假设了 的均匀分布,而实际情形并非如此.例如,回到我们熟悉的西瓜问题,考虑{假设 1: 好瓜件(色泽=*)八(根蒂=蜷缩)八(敲声=浊响)}和{假设 2: 好瓜村(色泽= *)^(根蒂=硬挺)^ (敲声:清脆)}.从 NFL 定理可知,这两个假设同样好.我们立即会想到符合条件的例子,对好瓜(色泽=青绿;娘蒂=蜷缩;敲声=浊响)是假设1更好,而对好瓜(色泽=乌黑;根蒂=硬挺;敲声=清脆)则是假设2更好.看上去的确是这样.然而需注意到, ” (根蒂=蜷缩;敲声=浊晌)”的好瓜很常见,而”(根蒂:硬挺;敲声 清脆)”的好瓜罕见,甚至不存在.
若要考虑所有的潜在问题,则所有的学习算法都一样好,要谈论算法的相对优劣,必须要针对具体的学习问题;在某些问题上表现好的学习算法,在另一些问题上却可能不尽如人意,学习算法自身的归纳偏好与问题是否相配,往往会起到决定性作用。
下面我们来讲归纳偏好——Inductive Bias
2 Inductive Bias
inductive bias:在机器学习中,很多学习算法经常会对学习的问题做一些关于目标函数的必要假设,称为归纳偏置,或称归纳偏好。但是我认为,中文翻译为归纳偏好更好。
由第一节可知,No-Free-Lunch认为没有先验知识进行学习是不可能的。如果我们不对特征空间有先验假设,则所有算法的平均表现是一样的。
通常情况下,我们不知道具体上帝函数的情况,但我们猜测它类似于一个比较具体的函数。这种基于先验知识对目标模型的判断就是归纳偏置(inductive bias)。归纳偏置所做的事情,是将无限可能的目标函数约束在一个有限的假设类别之中,这样,模型的学习才成为可能。其实,贝叶斯学习中的“先验(Prior)”这个叫法,可能比“归纳偏置”更直观一些。他是一些先验知识的融入后所做出的的针对模型的约束。
归纳(Induction)是自然科学中常用的两大方法之一(归纳与演绎, induction and deduction),指的是从一些例子中寻找共性、泛化,形成一个比较通用的规则的过程;
偏置(Bias)是指我们对模型的偏好。
通俗的来讲,归纳偏置可以理解为:
- 在现实生活中,我们会从观察到的现象中归纳出一定的规则(heuristics)
- 根据这些规则对模型做一定的约束,归纳偏置即变成了关于目标函数的必要假设
- 提出这个假设的目的是为了选择出更符合现实规则的模型。在此过程中,归纳偏置起到“模型选择”的作用(这个作用在下一小节作用中体现和叙述)
接下来我们来举一些具体的例子加深理解
- 对于图片分类这一任务,我们就要提取图片的特征,通过“归纳”,我们知道,自然界的物体都是具有局部不变形的特征,比如尺度缩放、平移、旋转都不会影响其语义信息,因为图片有这样的天然特征,所以我们创建了CNN模型(或者说一种算法)来处理这种数据,CNN 的 Inductive Bias 是 局部性 (Locality) (即空间相近的grid elements有联系而远的没有)和 空间不变性 (Spatial Invariance) / 平移等效性 (Translation Equivariance)(旋转、平移等操作不影响语义信息)。我们根据这个假设设置CNN具有kernel权重共享的性质。事实证明,这种模型在图像处理上具有很好的效果。
- 对于时间序列这种类型的任务,我们要提取时间序列的特征,通过“归纳”,我们知道,时间序列具有sequentiality(顺序性)序列顺序上的time steps有联系和time invariance(时间不变性)时间变换的不变性,根据该假设所设置的RNN具有权重共享的特性
如果说我们用RNN来处理图片数据,CNN来处理时序数据,效果肯定是不好的,因为RNN的归纳偏好和图片数据的特点不匹配,CNN的归纳偏好和时序数据不匹配,所以说,这印证了第一节里的最后一句话,“学习算法自身的归纳偏好与问题是否相配,往往会起到决定性作用。”
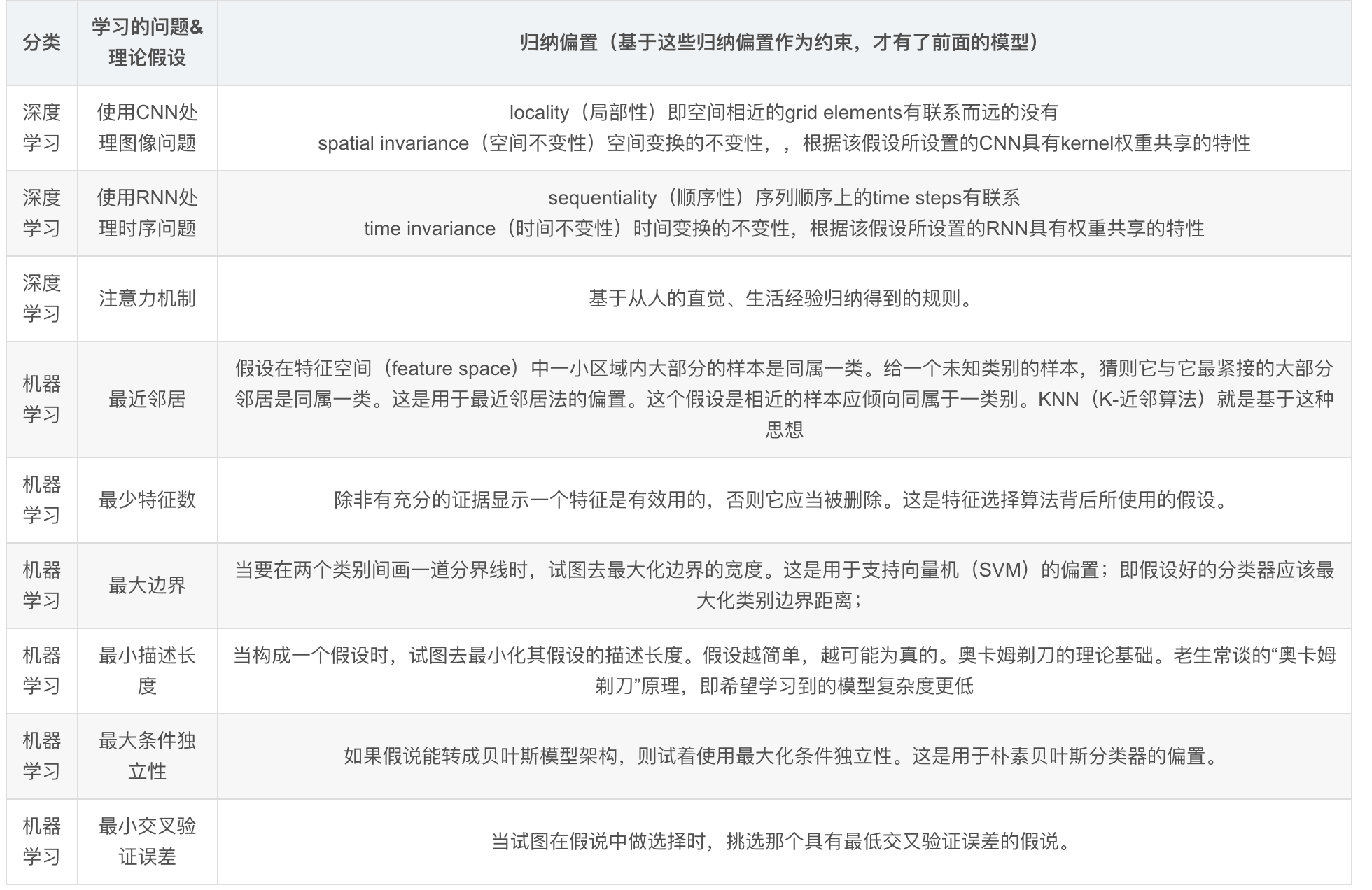
一些常见原理的归纳偏好: