预备知识:Batch Normalization
1 Batch Normalization局限性
假设把中国的收入水平进行标准化(变成标准正态分布),这时中国高收入人群的收入值接近3,中收入人群的收入值接近0,低收入人群接近-3。不难发现,标准化后的相对大小是不变的,即中国富人的收入水平在标准化前和标准化后都比中国穷人高。把中国的收入水平看成一个分布的话,我们可以说一个分布在标准化后,分布内的样本还是可比较的
假设把中国和印度的收入水平分别进行标准化,这时中国和印度的中收入人群的收入值都为0,但是这两个0可比较吗?印度和中国的中等收入人群的收入相同吗?不难发现,中国和印度的收入水平在归一化后,两国间收入值已经失去了可比性。把中国和印度的收入水平各自看成一个分布的话,我们可以说,不同分布分别进行标准化后,分布间的数值不可比较
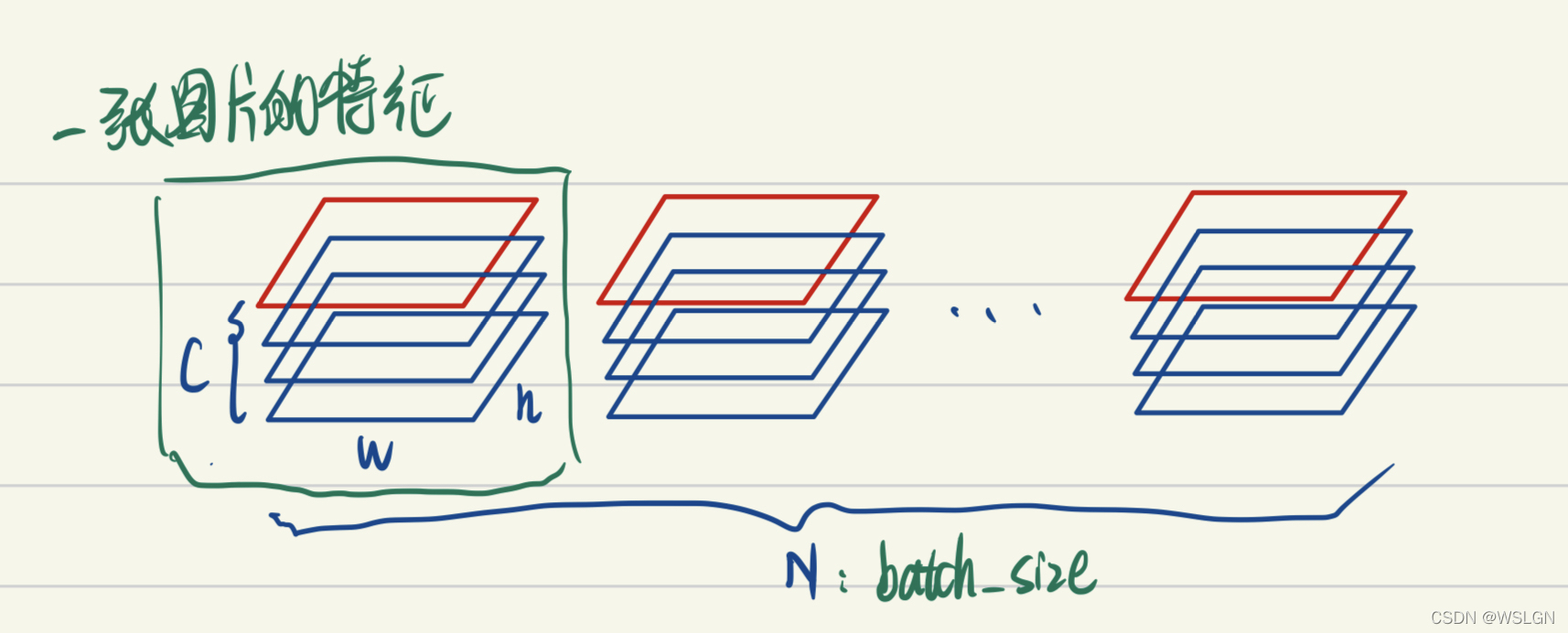
Batch Normalization就是把不同特征图的同一通道进行标准化,这就意味着:
- 不同图片的的同一通道的相对关系是保留的,即不同图片的同一通道的特征是可以比较的
- 同一图片的不同通道的特征则是失去了可比性
feature的每个通道都对应一种特征(如低维特征的颜色,纹理,亮度等,高维特征的人眼,鸟嘴特征等)。BatchNorm后不同图片的同一通道的特征是可比较的,或者说A图片的纹理特征和B图片的纹理特征是可比较的;而同一图片的不同特征则是失去了可比性,或者说A图片的纹理特征和亮度特征不可比较。
这其实是很好理解的,视觉的特征是比较客观的,一张图片是否有人跟一张图片是否有狗这两种特征是独立,即同一图片的不同特征是不需要可比性;而人这种特征模式的定义其实是网络通过比较很多有人的图片,没人的图片得出的,因此不同图片的同一特征需要具有可比性。也就是说BN在视觉领域是非常奏效的,因为其符合视觉特征图的内在特征。
但是在NLP领域呢?
比如说有个句子 ,“教练,我想打篮球!” 和 “老板,我要一打包子。”。通过比较两个句子中 “打” 的词义我们可以发现,词义并非客观存在的,而是由上下文的语义决定的。因此进行标准化时不应该破坏同一句子中不同词义向量的可比性,如果使用bn,就会破坏一个样本中特征之间的可比性,这是不对的,Layer Normalization可以解决这个问题
2 Layer Normalization
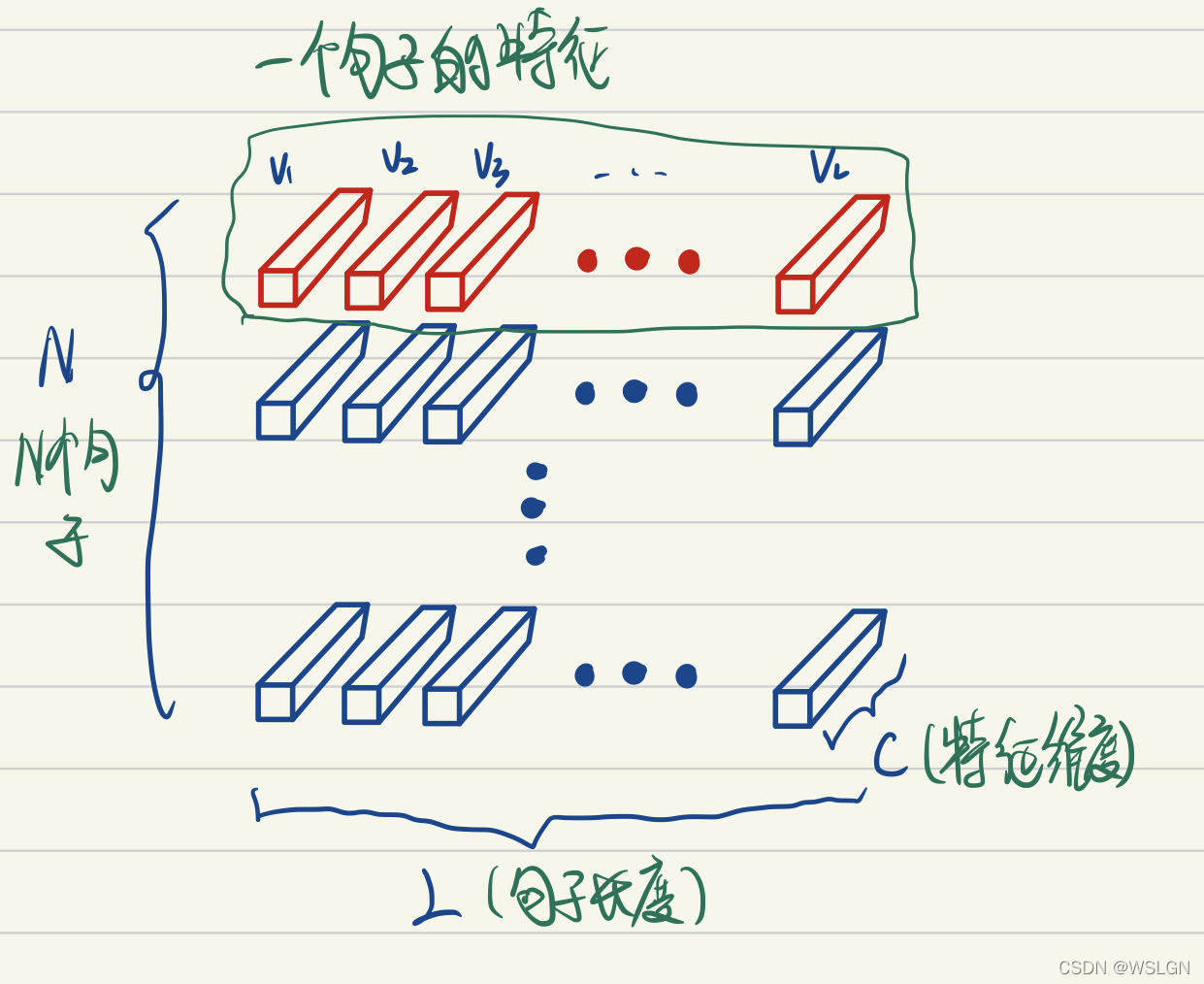
从上图可以看出Layer Norm是对每个样本进行标准化,而不是对所有样本的某一特征通道进行标准化,会保留同一句子不同单词之间的可比性,所以说Layer Norm更适合NLP任务。也就是说
- 同一句子中词义向量(上图中的V1, V2, …, VL)的相对大小是保留的,或者也可以说LayerNorm不改变词义向量的方向,只改变它的模。
- 不同句子的词义向量则是失去了可比性
- nn.BatchNorm2d(num_features)中的
num_features一般是输入数据的第2维(从1开始数)(也就是每个样本的通道数),BatchNorm中\(\gamma\)和\(\beta\)与num_features一致。在计算时,BN是把不同样本同一通道取出来,求平均值和方差的,然后对每个元素进行归一化,最后再乘以对应的γ 和β (每一通道共享)。BN共有num_features个mean和var,(假设输入数据的维度为(N,num_features, H, W))。- nn.LayerNorm(normalized_shape)中的
normalized_shape是最后的若干维,LayerNorm中weight和bias的shape就是传入的normalized_shape(normalized_shape可以理解为每一个样本的形状)。而LN是把normalized_shape这几个轴的元素展平,都放在一起,取平均值和方差的.然后对每个元素进行归一化,最后再乘以对应的γ和β(每个元素不同)。LN共有N1*N2个mean和var,γ和β在不同样本之间是共享的, γ,β.shape==normalized_shape(假设输入数据的维度为(N1,N2,normalized_shape),normalized_shape表示多个维度)
2.1 源码解析
pytorch官方文档对LayerNorm的解释:

结合具体例子来看
import torch import torch.nn as nn a=torch.empty(2,2,3).random_(0,3) print(a) #[batch_size=2,seq_len=2,emb_size=3]

对于每一个样本,其shape为[2, 3],也就是上文中说的normalized_shape。对于上述例子,pytorch的LayerNorm是如何处理的呢?对于每一个样本,扁平化然后z-score标准化,然后处理回原来的形状
- 扁平化

- 求其均值为1,方差为0.816496580927726
- z-score公式代入

- reshape回原先的形状
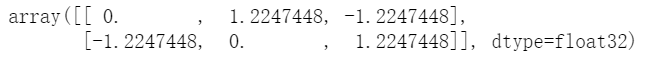
这就是这个batch中第一个数据LayerNormalization的结果,第二个数据也是重复这个流程
我们使用pytorch验证一下
ln=nn.LayerNorm([2,3])#2,3表示最后两个维度的大小,即为上文中的normalized_shape ln(a)

完全正确
如果我们的ln层定义为nn.LayerNorm(3),就不用展平了,直接对[1, 2, 0] [0, 1, 2]……进行标准化即可
对于nn.LayerNorm([2,3]),认为最后两个维度为一个layer,整个batch会有6对\(\gamma\)和\(\beta\),2对mean和variance;对于nn.LayerNorm(3),认为最后一个维度是一个layer,整个batch会有3对\(\gamma\)和\(\beta\),有2×2对mean和variance。
2.2 NLP中Layer Norm如何实现?
假设一个一个batch有16个句子,每个句子经过padding之后统一到10个单词,每个单词的embedding是256维,故一个batch的维度就是[16, 10, 256]。
在对这个句子进行layer norm的时候,我们是nn.LayerNorm([10, 256])还是nn.LayerNorm(256)呢?
一般采用的是后者,即对每个单词embedding进行标准化,而不是对整个句子所有单词embedding向量展平再标准化,因为每个序列(每个样本)的单词个数不一样,但在代码实现的时候会进行padding,比如一个序列原始单词数为10个,另一个序列原始单词数是8,然后你统一padding成了10个单词,那如果按照相同维度,进行归一化,norm的信息就会被无意义的padding的embedding冲淡的!这显然是不合理的。
3 RMSNorm
RMSNorm通过均方根的值缩放原始输入,保留原始均值信息,公式为:
\[y_i=\frac{x_i}{\mathrm{RMS}(x)}*\gamma_i,\quad\mathrm{~where~}\quad\mathrm{RMS}(x)=\sqrt{\epsilon+\frac{1}{n}\sum_{i=1}^nx_i^2}\]
LayerNorm会把输入的均值置为0,标准差为1。RMSNorm不改变均值,标准差不会变为1,但是会对数据的整体幅度整体幅度。
为什么现在大模型都采用RMSNorm?
- 参数量:RMSNorm的可学习参数量为LayerNorm的一半。
- 计算量:RMSNorm的计算量要比LayerNorm的计算量要少。
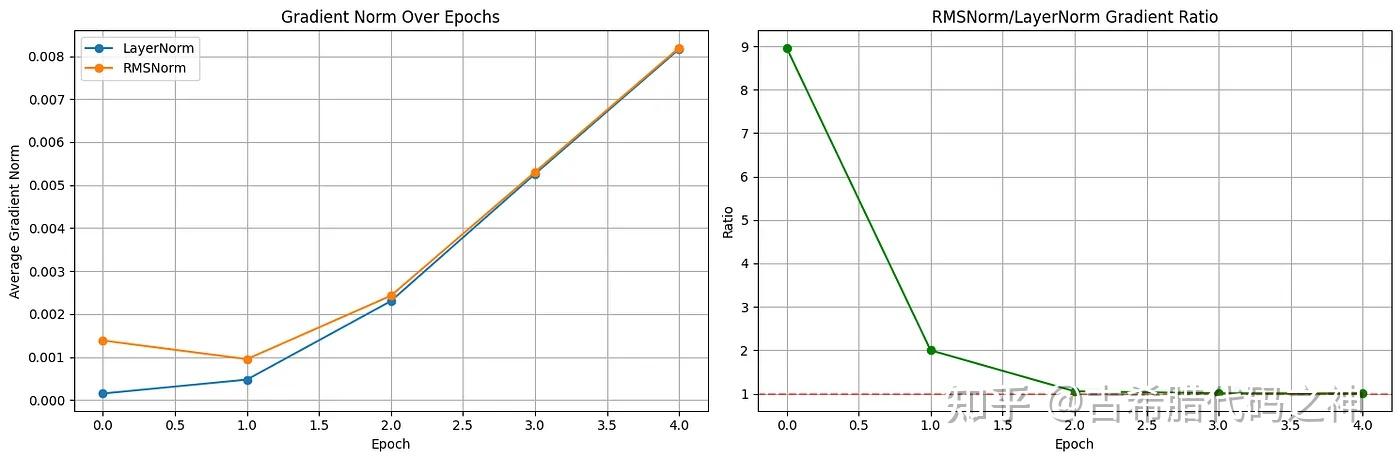
- 数值稳定性/梯度消失:LayerNorm输出值平均值为0可能会导致梯度在反向传播过程中消失,并且可以参考下图看到RMSNorm的梯度在Epoch之间相比LayerNorm更好。
4 Pre VS. Post Norm
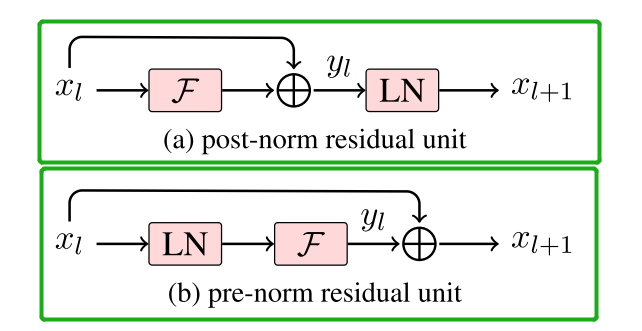
Post Norm:
在post norm里,根据链式求道法则,我们用loss对于\(x_l\)求导,\(L\)是l之后的某一层:
\[\frac{\partial\mathcal{L}}{\partial x^{(l)}}=\frac{\partial\mathcal{L}}{\partial x^{(L)}}\cdot\prod_{k=l}^{L-1}\frac{\partial x^{(k+1)}}{\partial x^{(k)}}\]
因为\(x^{(k+1)}=\mathrm{LN}(x^{(k)}+F(x^{(k)}))\),所以其中:
\[\frac{\partial x^{(k+1)}}{\partial x^{(k)}}=\frac{\partial\mathrm{LN}}{\partial z}\cdot(I+\frac{\partial F}{\partial x^{(k)}})\]
结合上述两个式子,也就有:
\[\frac{\partial\mathcal{L}}{\partial x^{(l)}}=\frac{\partial\mathcal{L}}{\partial x^{(L)}}\cdot\prod_{k=l}^{L-1}\frac{\partial\mathrm{LN}}{\partial z}\cdot(I+\frac{\partial F}{\partial x^{(k)}})\]
如果\(F\)是一个dense层,即 \(F=Wx\),那就会导致\(\frac{\partial F}{\partial x^{(k)}}=W\),如果\(W\)范数很大,因为一直链乘,会导致其梯度爆炸或消失
Pre Norm:
我们用和Post Norm同样的方式求导:
\[\frac{\partial\mathcal{L}}{\partial x^{(l)}}=\frac{\partial\mathcal{L}}{\partial x^{(L)}}\cdot\prod_{k=l}^{L-1}\frac{\partial x^{(k+1)}}{\partial x^{(k)}}\]
其中:
\[\frac{\partial x^{(k+1)}}{\partial x^{(k)}}=I+J^{(k)}, J^{(k)}=\frac{\partial F^{(k)}}{\partial\mathrm{LN}(x^{(k)})}\cdot\frac{\partial\mathrm{LN}(x^{(k)})}{\partial x^{(k)}}\]
从上式可以看出,链乘的是\(J=\frac{\partial F(\mathrm{LN}(x))}{\partial x}\),是对归一化的输入进行求导,相较于W,J的范数是比较稳定的,不会过大或者过小,经过系列连乘,梯度也不会爆炸活着消失,所以在现代大模型中,由于层数通常很深,大都采用Pre Norm。
为什么J的范数比较稳定?
在Pre Norm结构中:
\[x^{(l+1)}=x^{(l)}+F(\mathrm{LN}(x^{(l)}))\]
反向传播时:
\[\frac{\partial x^{(l+1)}}{\partial x^{(l)}}=I+J\quad J=\frac{\partial F(\mathrm{LN}(x))}{\partial x}=\frac{\partial F}{\partial u}\cdot\frac{\partial\mathrm{LN}}{\partial x}\]
首先,从\(\frac{\partial F}{\partial u}\)的角度考虑,通过LN,会保证F的输入会被压缩到统一的、尺度良好的空间中,F的导数是关于x的一个函数,这样一来,F的导数不会因为输入分布太奇怪而输出极端的梯度,有效的抑制了梯度爆炸或者消失。
其次,从\(\frac{\partial LN}{\partial x}\)的角度考虑,这个导数涉及均值和方差的偏导,但最终都除以标准差(即 sqrt(方差)),可以证明它的 谱范数(最大奇异值)≤ 1,因此不会导致梯度扩张。
5 参考资料
不理解的一个地方:“LN共有N1
*N2个mean和var,N1*N2*normalized_shape对γ和β(假设输入数据的维度为(N1,N2,normalized_shape)” 和 “对于nn.LayerNorm([2,3]),认为最后两个维度为一个layer,整个batch会有6对γ和β,2对mean和variance;对于nn.LayerNorm(3),认为最后一个维度是一个layer,整个batch会有3对γ和β,有2×2对mean和variance。” 这俩句话对不上啊。。γ和β的对数是咋算的到底。。应该是normalized_shape对γ和β才对吧对不起,我表述有误。在layernorm里,mean和var的数量应该等于样本的数量,也就是N1*N2。γ和β是一对可学习的参数,它们的数量LayerNorm 的 γ和β的 shape == normalized_shape,并且batch里所有样本共享同一套γ、β。比如normalized_shape=[2,3],那么γ和β的shape也为[2,3],也就是6对