论文地址:ECA-Net: Efficient Channel Attention for Deep Convolutional Neural Networks
1 Background
ECA-Net是SENet的改进,SENet在计算C个通道的attention score的时候,使用的是单隐藏层的MLP: C->C/r->C,作者认为,在计算attention时进行了降维(dimensionality reduction)会导致信息丢失,影响预测,并且不能很好地预测channels间的关系。虽然使用无隐藏层的C->C的MLP可以不用降维进行计算(论文中有计算,这种方式确实比SE要好),但是其参数数量为\(C^2\),计算开销比较大。由此,作者提出了ECA-Net,可以在少的参数的情况下,不降维地、跨通道地计算attention score,并且达到比较好的效果。
2 Proposed Method
2.1 pilot experiment
作者首先做了SE-var1,2,3这三个实验
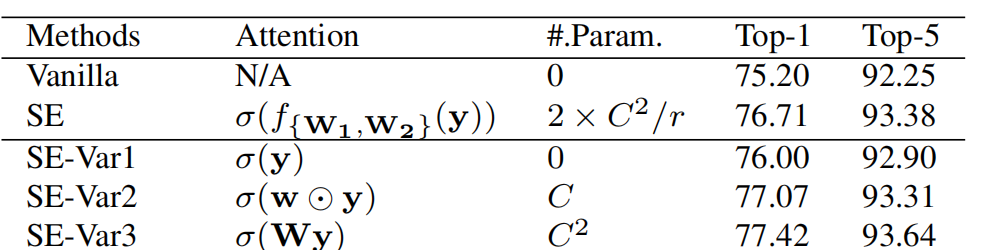
Var1参数数量为0,即把GAP得到的aggregated features经过一层sigmoid直接得到attention score。Var2参数数量为C,相比于Var1,它进行了一次点乘。Var3的参数数量为\(C^2\),就是在Background里的提到的无隐藏层的MLP,它没有进行dimensionality reduction,参数数量也很多,其效果也最好。
作者把SE-var2,3用下图的矩阵形式表示:
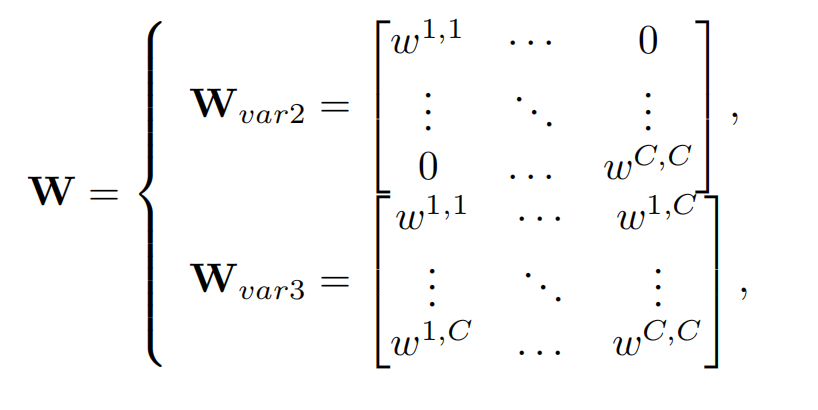
var2参数少,但是不能捕捉channel之间的相关性,var3虽然能捕捉channel间的相关性,但是参数数量很多。作者在var2和var3进行了折中,使用了分组的方式,即
\[\mathbf{W}_G=\begin{bmatrix}\mathbf{W}_G^1&\cdots&\mathbf{0}\\\vdots&\ddots&\vdots\\\mathbf{0}&\cdots&\mathbf{W}_G^G\end{bmatrix},\]
每一组有C/G个channels,每一组独立地计算attention。下图中的SE-GC就是这种计算方式的实验结果:
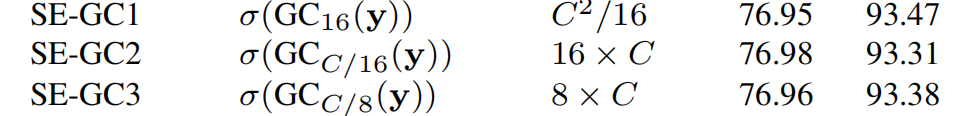
可以看出来这种分组的方式相比于Var2没有提升,因为其只在组内有交互,但是组间的channels没有沟通。由此,为了既能将所有channels之间产生联系,又能不降维,还保证计算复杂度,参数数量不高,作者提出了ECA。
2.2 Efficient Channel Attention (ECA) Module
2.2.1 version1
使用如下矩阵计算attention
\[\begin{bmatrix}w^{1,1}&\cdots&w^{1,k}&0&0&\cdots&\cdots&0\\0&w^{2,2}&\cdots&w^{2,k+1}&0&\cdots&\cdots&0\\\vdots&\vdots&\vdots&\vdots&\ddots&\vdots&\vdots&\vdots\\0&\cdots&0&0&\cdots&w^{C,C-k+1}&\cdots&w^{C,C}\end{bmatrix}.\]
有k×C个参数,上述计算方式解决了组之间没有关联这一问题。
\[\omega_i=\sigma\Big(\sum_{j=1}^kw_i^jy_i^j\Big),y_i^j\in\Omega_i^k,\]
2.2.2 version2
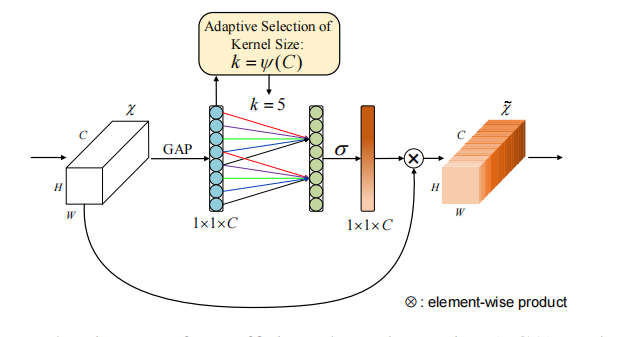
相较于version1,一个更精简的方式是让所有的channel共享一套参数(这也是最终ECA的实现方式),即:
\[\omega_i=\sigma\bigg(\sum_{j=1}^kw^jy_i^j\bigg),y_i^j\in\Omega_i^k.\]
\(\Omega_i^k\)表示channel \(y_{i}\)周围的k个临近channels。由于共享参数,参数是所有通道共同一起学习得到的,所以相当于每个通道可以和其它所有通道进行interact。这种计算方式,其实就是1D Convolution,即:
\[\omega=\sigma(\operatorname{C1D}_k(\mathbf{y})),\]
2.3 Coverage of Local Cross-Channel Interaction
首先,channel数量和ECA的覆盖范围k成线性关系是不够的,表示能力非常有限,要加入一些非线性,又因为channel的数量通常是2的整数幂,所以作者定义如下关系:
\[C=\phi(k)=2^{(\gamma*k-b)}.\]
即:
\[k=\psi(C)=\left|\frac{log_2(C)}\gamma+\frac b\gamma\right|_{odd},\]
显然,通过映射\(\psi\),channel数量多的特征具有更长的coverage(k),而channel数量少的特征通过使用非线性映射具有更小的coverage。