论文地址：Drop an Octave: Reducing Spatial Redundancy in Convolutional Neural Networks with Octave Convolution

1 Introduction

图片可以被分解为低空间频率和高空间频率的部分，它们分别描述缓慢变化的结构和剧烈变化的详细细节。作者认为卷积层输出的特征图可以被分解为不同的空间频率。借此，作者提出了能够存储高频和低频特征图的特征表示方法，并且提出了可以处理这种特征表示的卷积：Octave Convolution。通过这些处理，低频的特征图的空间分辨率可以安全地减少，因为低频中临近区域的信息是共享的。

OctConv优势：

• 由于减少了低频特征图的分辨率，减少了空间信息的冗余，不仅节约了内存，还节约了计算
• 在计算低频输出的时候（H->L），增加可感受野，提高了识别效果

2 Octave Feature Representation

传统方法中，所有输入输出的特征图都是相同的空间分辨率，这是非必要的，因为一些channels可能包含的是低频特征，它们是空间冗余的，是有压缩空间的。

为了解决这个问题，作者提出了Octave Feature Representation，把feature maps分解为两组，分别是低频和高频。把特征图\(X\)在通道维度进行分解\(X=\{X^{H},X^{L}\}\)，\(X^H\in\mathbb{R}^{(1-\alpha)c\times h\times w}\)

3 Octave Convolution

Octave Conv的设计目标就是在低频和高频分别处理特征图，节约计算，并且还能实现低频高频特征图之间的交流。

输出是\(Y=\{Y^{H},Y^{L}\}\)，高频和低频都由两个流进行计算，\(Y^{H}=Y^{H\rightarrow H}+Y^{L\rightarrow H}\mathrm{and}Y^{L}=Y^{L\rightarrow L}+Y^{H\rightarrow L}\)。同样，对于卷积核也分为两组\(W=[W^{H},W^{L}]\)，分别处理高频和低频特征图

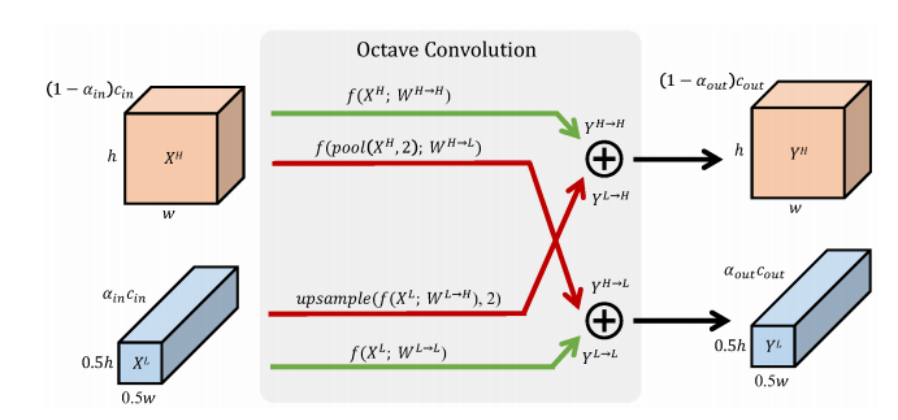
对于高频特征图输出\(Y^H\)，\((p,q)\)位置处由如下方式计算

\[\begin{aligned}
Y_{p,q}^{H}& =Y_{p,q}^{H\rightarrow H}+Y_{p,q}^{L\rightarrow H} \\
&= =\sum_{i,j\in\mathcal{N}_{k}}W_{i+\frac{k-1}2,j+\frac{k-1}2}^{H\to H}X_{p+i,q+j}^{H} \\
&+\sum_{i,j\in\mathcal{N}_k}W_{i+\frac{k-1}2,j+\frac{k-1}2}^{L\to H}X_{(\lfloor\frac p2\rfloor+i),(\lfloor\frac q2\rfloor+j)}^{L},
\end{aligned}\]

对于低频特征图输出\(Y^L\)，\((p,q)\)位置处由如下方式计算

\[\begin{aligned}
\begin{gathered}Y_{p,q}\end{gathered}& \begin{aligned}=&Y_{p,q}^{L\to L}+Y_{p,q}^{H\to L}\end{aligned} \\
&=\sum_{i,j\in\mathcal{N}_k}W_{i+\frac{k-1}2,j+\frac{k-1}2}^{L\to L}X_{p+i,q+j}^{L} \\
&+\sum_{i,j\in\mathcal{N}_k}W_{i+\frac{k-1}2,j+\frac{k-1}2}^{H\to L}X_{(2*p+0.5+i),(2*q+0.5+j)}^{H},
\end{aligned}\]

代码如下：

class OctaveConv(nn.Module):
def __init__(self, in_nc, out_nc, kernel_size, alpha=0.5, stride=1, dilation=1, groups=1, \
bias=True, pad_type='zero', norm_type=None, act_type='prelu', mode='CNA'):
super(OctaveConv, self).__init__()
assert mode in ['CNA', 'NAC', 'CNAC'], 'Wong conv mode [{:s}]'.format(mode)
padding = get_valid_padding(kernel_size, dilation) if pad_type == 'zero' else 0
self.h2g_pool = nn.AvgPool2d(kernel_size=(2, 2), stride=2)
self.upsample = nn.Upsample(scale_factor=2, mode='nearest')
self.stride = stride

self.l2l = nn.Conv2d(int(alpha * in_nc), int(alpha * out_nc),
kernel_size, 1, padding, dilation, groups, bias)
self.l2h = nn.Conv2d(int(alpha * in_nc), out_nc - int(alpha * out_nc),
kernel_size, 1, padding, dilation, groups, bias)
self.h2l = nn.Conv2d(in_nc - int(alpha * in_nc), int(alpha * out_nc),
kernel_size, 1, padding, dilation, groups, bias)
self.h2h = nn.Conv2d(in_nc - int(alpha * in_nc), out_nc - int(alpha * out_nc),
kernel_size, 1, padding, dilation, groups, bias)
self.a = act(act_type) if act_type else None
self.n_h = norm(norm_type, int(out_nc*(1 - alpha))) if norm_type else None
self.n_l = norm(norm_type, int(out_nc*alpha)) if norm_type else None

def forward(self, x):
X_h, X_l = x

if self.stride ==2:
X_h, X_l = self.h2g_pool(X_h), self.h2g_pool(X_l)

X_h2h = self.h2h(X_h)
X_l2h = self.upsample(self.l2h(X_l))
X_l2l = self.l2l(X_l)
X_h2l = self.h2l(self.h2g_pool(X_h))

#print(X_l2h.shape,"~~~~",X_h2h.shape)
X_h = X_l2h + X_h2h
X_l = X_h2l + X_l2l

if self.n_h and self.n_l:
X_h = self.n_h(X_h)
X_l = self.n_l(X_l)

if self.a:
X_h = self.a(X_h)
X_l = self.a(X_l)

return X_h, X_l

4 Application

将OctConv融入骨干网络，在第一层卷积中，设置\(\alpha_{in}=0\mathrm{and}\alpha_{out}=\alpha.\)，这样，得到的输出全是low frequency的了，为了把multi-frequency转换回去，设置\(\alpha_{out}=0\)，这样会得到一个单一的全分辨率的输出。