论文链接:ShapeConv: Shape-aware Convolutional Layer for Indoor RGB-D Semantic Segmentation
1 Why ShapeConv for RGB-D tasks
深度图包含物体的基础形状(局部信息,local geometry)和物体的位置(全局信息,在更大的context下的信息)。但是用传统卷积去卷深度特征图会带来问题。

如上图所示,第一行中凳子上的两个红色横线,经过第二行的两个红色卷积核p1,p2卷积过后(绿色同理),由于深度图中的像素值不同,会导致卷积结果不同,这会削弱网络对形状的感知,我们实现形状不变性,即对于形状相同的物体,经过卷积输出的结果应该相同,但是传统卷积也不能丢弃,因为具有相同形状的物体不能输出一样,因为他们的位置会不同,这也是学习的一部分。因此作者设计了ShapeConv,将卷积分成base, shape component两个部分,分别负责处理where the patch is(位置信息)和what the patch is(形状信息,或者说叫物体的inherent property)
2 Method
例子图中的p1,p2像素值是不同的,相应地,它们的特征图也会不同,就会导致不同的分割结果,但是事实上,这两个patch之间也存在一些不变量,即为形状。因此,作者把每个卷积窗口的输入\(\mathbb{P}\in R^{K_{h}\times K_{w}\times C_{in}}\)分成两个component,base-component \(\mathbb{P}_{B}\)和shape-component \(\mathbb{P}_{S}\)。
2.1 ShapeConv Formulation
\[\begin{aligned}&\mathbb{P}_B=m(\mathbb{P}),\\&\mathbb{P}_{S}=\mathbb{P}-m(\mathbb{P}),\end{aligned}\]
\(m\)是平均操作,\(\mathbb{P}_B\in R^{1\times1\times C_{in}}\),\(\mathbb{P}_S\in R^{K_{h}\times K_{w}\times C_{in}}\),\(\mathbb{P}_{B}\)会代表patch的位置,\(\mathbb{P}_{S}\)会代表patch的固有特征,这样一来,相同形状的物体尽管在不同的位置,它们的\(\mathbb{P}_{S}\)是相同的,但同时位置信息也不会丢弃,因为有\(\mathbb{P}_{B}\)。
作者用两组weight来处理这两个components,分别是\(\mathbb{W}_B\in R^1\)和\(\mathbb{W}_{S}\in R^{K_{h}\times K_{w}\times K_{h}\times K_{w}\times C_{in}}\),输出的结果会做相加,然后再用传统卷积的卷积核去卷它们。总体过程如下:
\[\begin{aligned}
\text{F}& =ShapeConv(\mathbb{K},\mathbb{W}_B,\mathbb{W}_S,\mathbb{P}) \\
&=Conv(\mathbb{K},\mathbb{W}_B\diamond\mathbb{P}_B+\mathbb{W}_S*\mathbb{P}_S) & \text{(1)} \\
&=Conv(\mathbb{K},\mathbf{P_B}+\mathbf{P_S}) \\
&=Conv((\mathbb{K},\mathbf{P_{BS}}),
\end{aligned}\]
\(\mathbf{P_B}, \mathbf{P_S}\)的计算过程如下所示
\[\begin{cases}\mathbf{P_B}=\mathbb{W}_B\diamond\mathbb{P}_B\\\mathbf{P_{B_{1,1,c_{in}}}}=\mathbb{W}_B\times\mathbb{P}_{B_{1,1,c_{in}}},\end{cases}\\\begin{cases}\mathbf{P_S}=\mathbb{W}_S*\mathbb{P}_S\\\mathbf{P_{S_{k_h,k_w,c_{in}}}}=\sum_i^{K_h\times K_w}(\mathbb{W}_{S_{i,k_h,k_w,c_{in}}}\times\mathbb{P}_{S_{i,c_{in}}}),\end{cases}\]
\(\mathbf{P_B}\)的计算方式很简单,就是直接相乘。接下来讲下\(\mathbf{P_S}\)的计算。对于\(\mathbf{P_S}\)中坐标为\((k_{h} ,k_{w} ,c_{in})\)的每个点,都由\(\mathbb{P}_{S_{i,c_{in}}}\in R^{K_{h}\times K_{w}}\)和\(\mathbb{W}_{S_{i,k_h,k_w,c_{in}}}\in R^{K_{h}\times K_{w}}\)相乘然后累加得到。然后\(\mathbf{P_B}, \mathbf{P_S}\)相加会得到\(\mathbf{P_BS}\),其内涵重要的形状信息,这是普通卷积做不到的。
2.2 Training and Inference
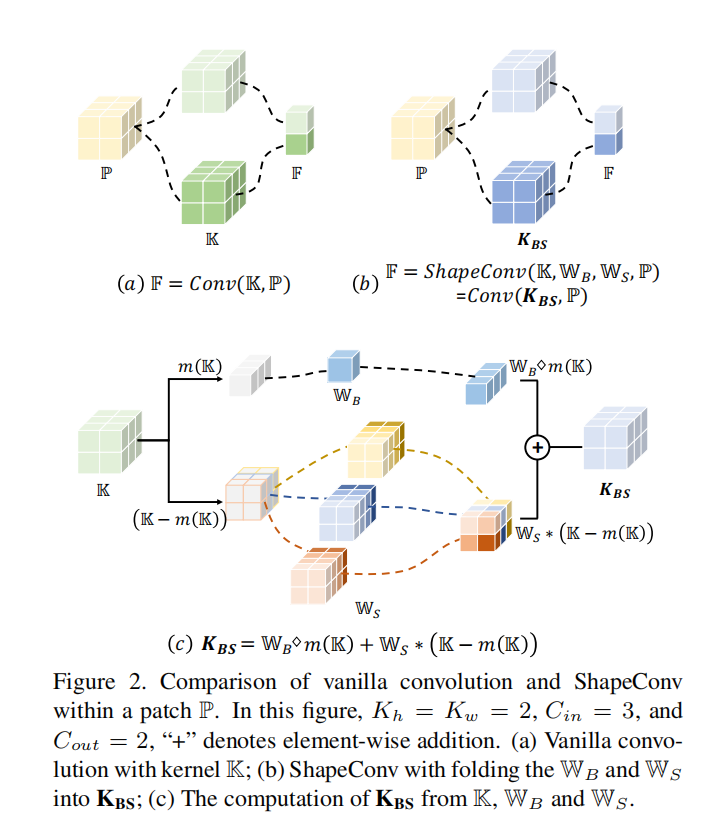
从上面的运算过程可以看出,ShapeConv比普通卷积要多两个weights的product操作,会增加时间开销,因此作者把这两个乘积操作shift from patches to kernels,对卷积核进行weight product操作。
\[\begin{cases}\mathbf{K_B}=\mathbb{W}_B\diamond\mathbb{K}_B\\\mathbf{K_{B_{1,1,c_{in},c_{out}}}}=\mathbb{W}_B\times\mathbb{K}_{B_{1,1,c_{in},c_{out}}},\end{cases}\\\begin{cases}\mathbf{K_S}=\mathbb{W}_S*\mathbb{K}_S\\\mathbf{K_{S_{k_h,k_w,c_{in},c_{out}}}}=\sum_i^{K_h\times K_w}(\mathbb{W}_{S_{i,k_h,k_w,c_{in}}}\times\mathbb{K}_{S_{i,c_{in},c_{out}}}),\end{cases}\]。据此,可以重新定义ShapeConv:
\[\begin{aligned}
\text{F}& =ShapeConv(\mathbb{K},\mathbb{W}_B,\mathbb{W}_S,\mathbb{P}) \\
&=Conv(\mathbb{W}_B\diamond m(\mathbb{K})+\mathbb{W}_S*(\mathbb{K}-m(\mathbb{K})),\mathbb{P}) \\
&=Conv(\mathbb{W}_B\diamond\mathbb{K}_B+\mathbb{W}_S*\mathbb{K}_S,\mathbb{P})& \text{(2)} \\
&=Conv(\mathbf{K_B}+\mathbf{K_S},\mathbb{P}) \\
&=Conv(\mathbf{K_{BS}},\mathbb{P}),
\end{aligned}\]
经过数学推导(此处略),公式(1)和(2)是等价的。这样一来,ShapeConv和普通卷积的复杂度一致,没有带来额外的推理时间,仅在训练时多训练了两组weights。
2.3 ShapeConv Newtwork
作者用ShapeConv去替换网络中的普通卷积,同时\(\mathbb{W}_B, \mathbb{W}_S\)都被初始化为恒等矩阵,可以让ShapeConv利用pretrained models里已经训练好的参数。