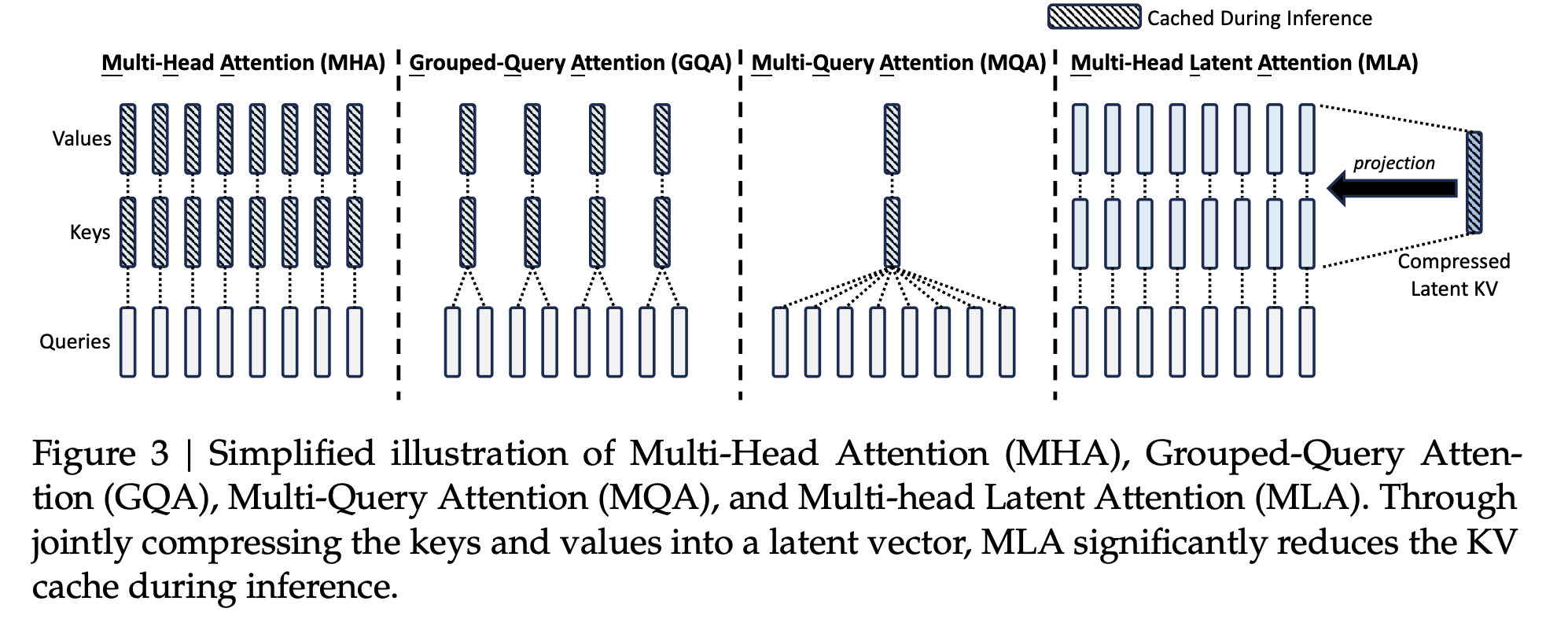
这一篇,我会按照KV Cache的原理、LLM推理阶段KV Cache显存占用分析以及如何优化推理阶段KV Cache的显存占用的顺序去讲解。
参考:
deepseek技术解读(1)-彻底理解MLA(Multi-Head Latent Attention)
1 KV Cache
1.1 不使用KV Cache
给定“天气”,模型会逐个预测剩下的字,假设接下来预测的两个字为“真好“。
注意:下面的示例图只给出了和 KV Cache 相关的细节。
第一步会预测”真“
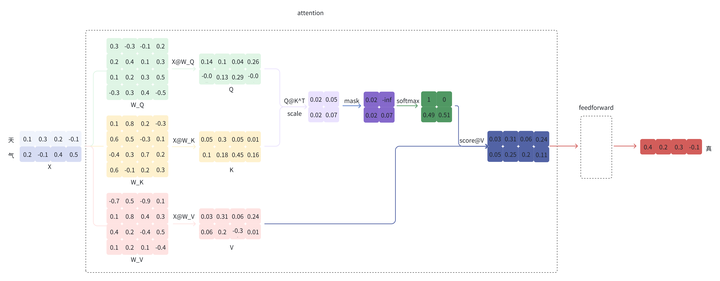
output 再经过 feedforward 等步骤最终得到预测的 token ”真“;
第二步会将”真“拼接到”天气“的后面,即新的输入为”天气真“,再预测”好“
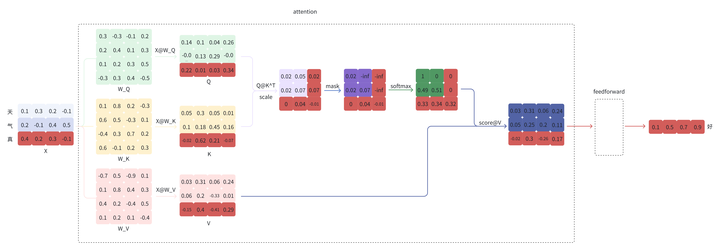
同样的,output 再经过 feedforward 等步骤最终得到预测的 token ”好“;
1.2 使用KV Cache
观察上面的计算过程,可以看到,在第二步的预测中,”好“的预测只和”真“以及完整的 K, V 有关,“天”,“气”这两个查询和“好”的predicton没有任何关系。于是,KV Cache 的想法就很直观了,缓存上一轮的 K, V,即可达到减少计算,提速的效果,是一种用空间换时间的方式。
从第二步开始时,只需输入当前位置的 token,得到当前位置对应的 K_cur, V_cur,再拼接上一步缓存的 K_last, V_last 得到完整的 K, V,即可完成下一个 token 的预测。下图是在上图的基础上只保留和预测”好“相关的数据:
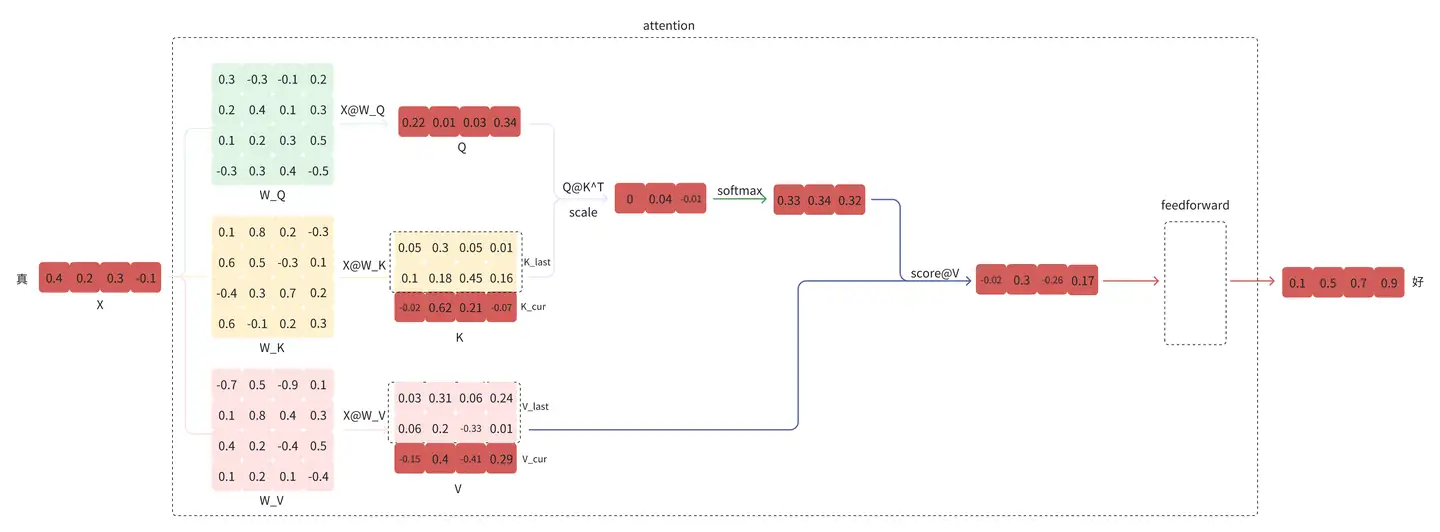
1.3 总结
KV-cache本质是通过空间换时间的方法。我们知道当前LLM size都比较大,GPU的显存空间也是比较宝贵的,通过显存来保存KV-cache势必会带来访存的瓶颈。换句话说,如果不用KV-cache模型直接计算(重复计算前序kv ),是个计算密集型任务;增加了KV-cache,现在不是通过计算得到kv,而是从「存储介质」里读出来,GPT内核与存储介质之间要频繁读写,这样就变成了一个访存密集型任务。所以使用了KV-cache的机制,解决的重复计算的问题,但访存的速率也就直接影响到训练和推理的速度。
2 LLM推理阶段KV Cache显存占用分析
2.1 访存速率分级
以分布式推理结构为例:
比如2台机器,每台机器有8张A100, 那么在这样一个系统内,卡内,单机卡间,机器之间的数据访问效率如图3所示。
注:我们的例子中,只描述了一种访存介质HBM (也就是我们常说的显卡的显存),我们知道通常GPU的存储介质除了显存,还有SRAM和DRAM。SRAM也被成为片上存储,是GPU计算单元上即时访问更快的存储,所有的计算都要先调度到片上存储SRAM才能做计算,一般只有几十M大小,带宽可达到20T/s左右,SRAM是跟计算单元强绑定的,推理阶段一般不考虑将SRAM作为存储单元使用。而DRAM是我们常说的CPU的内存,由于访问速率较慢,推理阶段一般也不考虑使用。所以我们讨论的推理存储介质,一般就指的是HBM(显存)
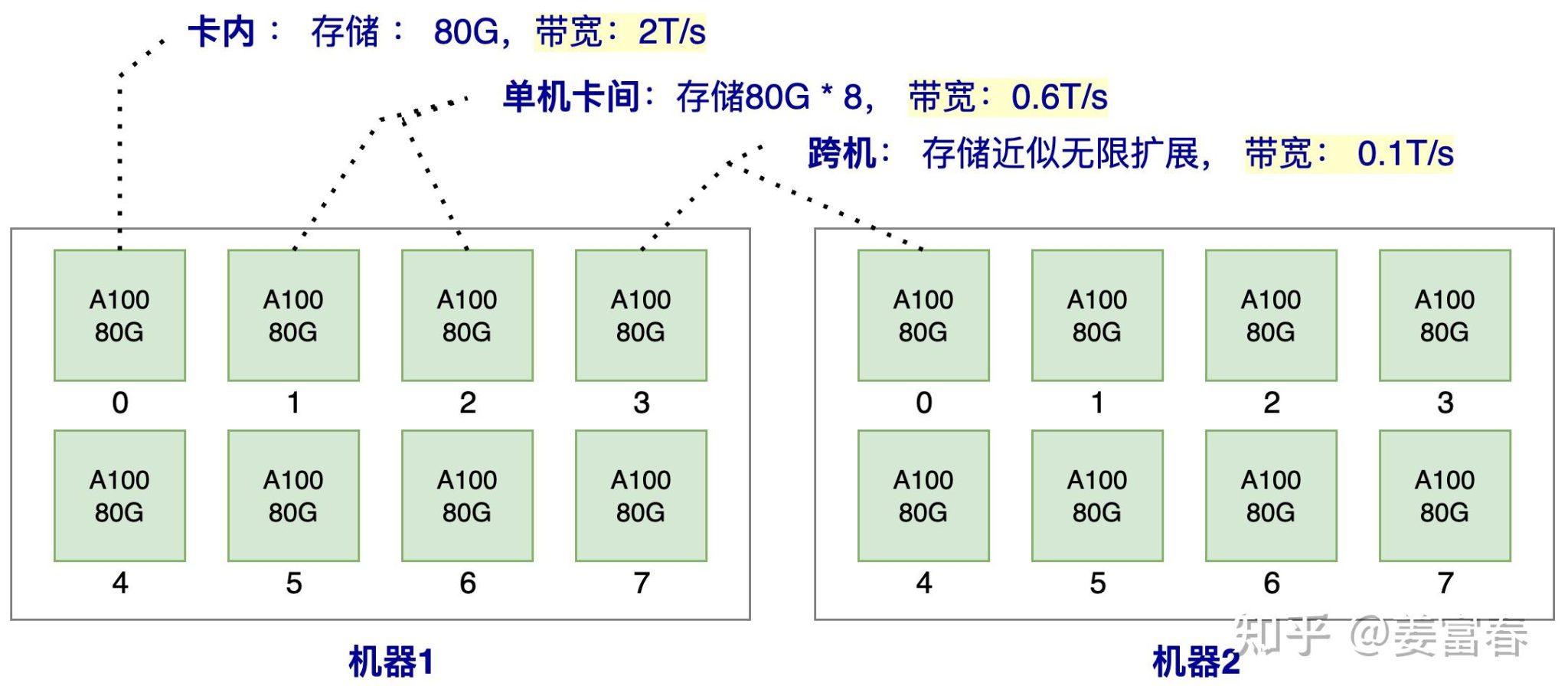
由上图的访存带宽可知,卡内的带宽是单机卡间的带宽的3倍,是跨机带宽的20倍,所以我们对于存储的数据应该优先放到卡内,其次单机内,最后可能才考虑跨机存储。
接下来我们再看下,推理过程中,有哪些数据要存储到显存上。
2.2 模型推理阶段显存分配
推理阶段主要有三部分数据会放到显存里:
- KV Cache :前序token序列计算的k,v结果,会随着后面tokent推理过程逐步存到显存里。存储的量随着Batch,Sequence_len长度动态变化
- 模型参数:包括Transformer、Embedding等模型参数会存到显存里。模型大小固定后,这个存储空间是固定的。
- 运行时中间数据: 推理过程中产出的一些中间数据会临时存到显存,即用即释放,一般占用空间比较小
由上述可知,推理阶段主要存储消耗是两部分: 模型参数和 KV Cache。那么模型参数占多少,KV Cache又占多少?
我们现在看看对于单个token,其KV Cache要占用多少显存空间。
以Qwen-72B为例,但不考虑其GQA的设置,计算的是传统的MHA,Qwen-72B模型80层,64个head,每个head有128维度,即:\(l=80,n_{h}=64,d_{h}=128\)
对于每一层,都要存储一个k,v,所以针对一个token,其缓存的k,v的数量为:
\[num_{kv}=2*l*n_{h}=2\times(80\times64)_{qwen_72B}=10240\]
假设模型推理是半精度bf16,即单个数字占用2byte,一个token产生的KV Cache所占用的显存为:
\[1token_mem_{kv}=2*num_{kv}*d_{h}=2\times(10240\times128)_{qwen_72B}=2.62(MB)\]
我们现在知道了一个Token计算后需要缓存的kv数量和存储量。那么对于一个实际的推理场景,还要考虑批量Batch(B)和 序列长度Sequence_len(S) 两个维度,来确认整体KV Cache的存储消耗。这两个维度通常是可以动态变化的。我们看看下面两个场景:
场景1:单条短文本场景
BatchSize=1,S=2048,其KV Cache占用显存为:
\[\begin{aligned}
mem_{kv}=1token_mem_{kv} & *B*S=(2.62(MB)\times1\times2048)_{qwen_7{2B}} \\
& =5.366GB
\end{aligned}\]
场景2:并发长文本场景
BatchSize=32,S=4086,其KV Cache占用显存为:
\[\begin{aligned}
mem_{kv}=1token_mem_{kv}*B*S & =(2.62(MB)\times32\times4096)_{qwen_{72B}} \\
& =343.4GB
\end{aligned}\]
除了KV Cache,推理时,模型参数也要占用显存空间,我们设模型参数量为\(\mathbf{\Phi}\),对于半精度BF16,其占用字节数为\(2\mathbf{\Phi}\),对于Qwen-72B,其占用显存为:
\[mem_p=2*\Phi=2\times(72)_{qwen_72B}=144G\]
我们再结合上面两个场景,看看显存的整体分配:
- 场景1: 模型存储需要144G,KV Cache需要5.366G,模型的参数储存占主导,使用80G的A100, 至少需要2张卡做推理。
- 场景2:模型存储需要144G,KVCache需要343.4G,KV Cache储存占主导,使用80G的A100, 至少需要7张卡做推理
这里还要多啰嗦几句,推理阶段根据离线、在线的业务场景,到底组多大的Batch,其实是一个Balance的过程,Batch选择比较小,虽然并发度不高,但可能单卡就能装下完整模型参数和KV Cache,这时候卡内带宽会比较高,性能可能依然出众,可以考虑适当增加Batch把单卡显存用满,进一步提升性能。但当Batch再增大,超出单卡范围、甚至超出单机范围,此时并发会比较大,但跨卡或跨机访存性能会降低,导致访存成为瓶颈,GPU计算资源使用效率不高,可能实际导致整体推理性能不高。所以单从推理Batch设置角度来看,要实测找到性能最佳的平衡点。
当前LLM都比较大,而访存的容量和访存速率有分级的特点。所以推理过程中,减少跨卡、卡机的访存读写是优化推理性能的一个有效路径。一方面单次读写的数据越少,整体速度会越快;另一方面整体显存占用越少,就能尽量把数据放到单卡或单机上,能使用更高的带宽读写数据。
3 如何优化推理阶段KV Cache的显存占用
3.1 优化方法汇总
方法主要有四类:
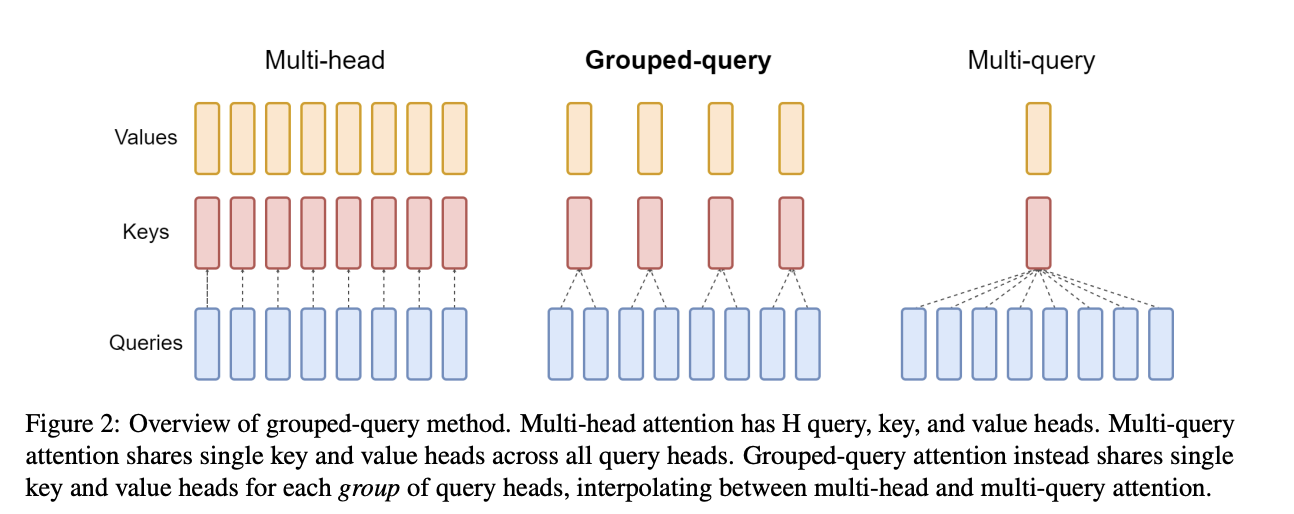
- 共享KV:多个Head共享使用1组KV,将原来每个Head一个KV,变成1组Head一个KV,来压缩KV的存储。代表方法:GQA,MQA等
- 窗口KV:针对长序列控制一个计算KV的窗口,KV cache只保存窗口内的结果(窗口长度远小于序列长度),超出窗口的KV会被丢弃,通过这种方法能减少KV的存储,当然也会损失一定的长文推理效果。代表方法:Longformer等
- 量化压缩:基于量化的方法,通过更低的Bit位来保存KV,将单KV结果进一步压缩,代表方法:INT8等
- 计算优化:通过优化计算过程,减少访存换入换出的次数,让更多计算在片上存储SRAM进行,以提升推理性能,代表方法:flashAttention等
这里我们主要讲第一种,共享KV,涉及GQL,MQA,MLA
3.2 共享KV优化Cache方法
3.2.1 MQA
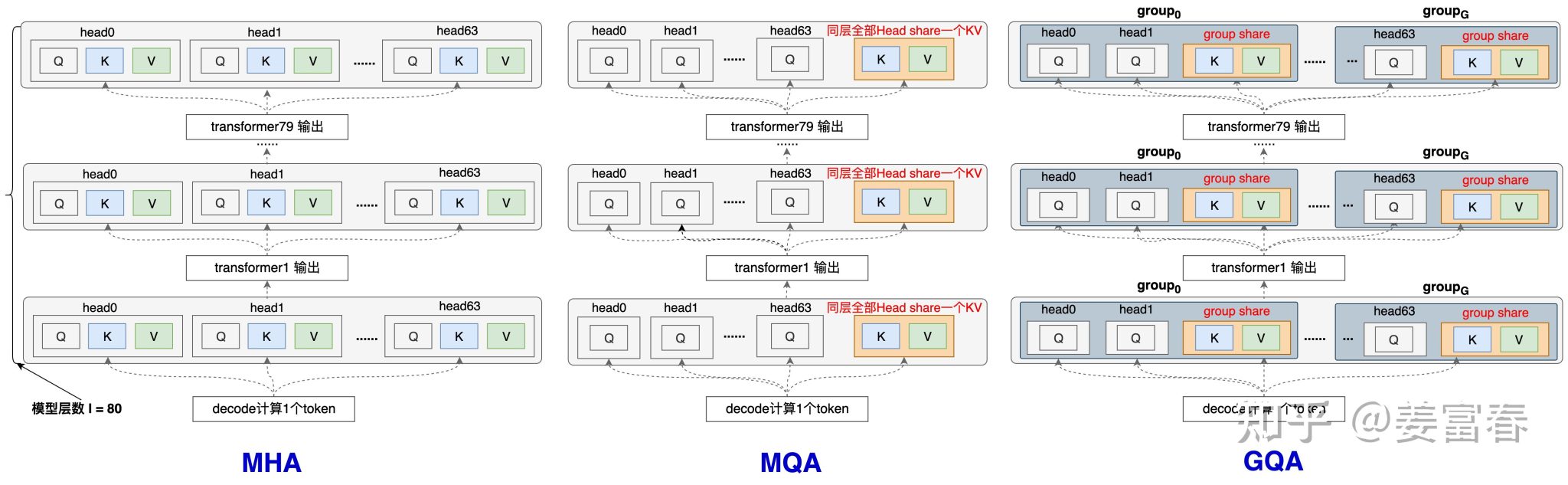
MQA方法比较简单,详见上图6最右侧的图,每一层的所有Head,共享同一个K,V来计算Attention。相对于MHA的单个Token需要保存的KV数\((\mathrm{~}2*l*n_h\mathrm{~})\)减少到了\((\mathrm{~}2*l)\)
3.2.2 GQA
GQA是平衡了MQA和MHA的一种折中的方法,不是每个Head一个KV,也不是所有Head共享一个KV,而是对所有Head分组,比如分组数为\(g\),那么每组\(n_h/g\)个head共享同一对kv。
为了方便自己更清晰的理解GQA和MQA ,以一个Token计算KV过程(如图5),画了一些相对细节展开的图,把所有层都画出来,并且加了一些注释:
3.2.3 MLA
MLA的核心就是用低秩的压缩表示来存储KV Cache,推理时减少显存占用。以下讨论均是从单个token的视角展开的。
3.2.3.1 变量命名说明
- \(d_h\):每个head的维度
- \(d_c\):MLA的低秩压缩的维度,论文中为\(4d_h\)
- \(n_h\):head的数量
- \(d\):隐层维度,\(d=d_h\times n_h\)
- \(h_t\):在某个attention layer里第t个token,维度为\(d\)
3.2.3.2 KV Cache都要存储什么?
我们在这里探讨t时刻的token \(h_t\),MLA是如何表达、存储它的key、value的。
\[\mathbf{c}_t^{KV}=W^{DKV}\mathbf{h}_t\]
其中\(W^{DKV}\in\mathbb{R}^{d_c\times d}\),是下采样投影矩阵,它把\(d\)维的token投影成\(d_c\),把以低秩的形式存储\(\mathbf{c}_t^{KV}\),节省空间。
3.2.3.3 Key、Value如何计算?
首先通过上采样矩阵将\(\mathbf{c}_t^{KV}\)投影回\(d\),生成K、V:
\[[\mathbf{k}_{t,1}^C;\mathbf{k}_{t,2}^C;…;\mathbf{k}_{t,n_h}^C]=\mathbf{k}_t^C=W^{UK}\mathbf{c}_t^{KV}\]
\[[\mathbf{v}_{t,1}^C;\mathbf{v}_{t,2}^C;…;\mathbf{v}_{t,n_h}^C]=\mathbf{v}_t^C=W^{UV}\mathbf{c}_t^{KV}\]
其中\(W^{UK},W^{UV}\in\mathbb{R}^{d_hn_h\times d_c}\),这样每个head就有一对单独的kv,而不像GQA、MQA一样,一对key value被多个query共享。
注:经过上述的变换,非常类似LoRA做低参数微调的逻辑。通过两个低秩矩阵先做压缩、再做扩展,最终能降低参数的数量。但MLA本质是要做到减少KV-cache的存储。LoRA强调的是参数量的减少,类似MLA这操作确实也减少了参数量,按DeepSeek-V3的参数配置,两个低秩矩阵参数量:\(2\times d_c\times d=2\times512\times7168\);而正常MHA的参数矩阵参数量:\(d\times d=7168\times7168\)
3.2.3.4 Query的计算过程
也类似于KV的逻辑,先投影到低维,在投影回高维,其实对于Query,因为它不涉及Cache,所以使用\(d \times d\)的q_proj也可以,但是DeepSeek-v3还是做了两次投影,感觉出于以下两个考虑:1)为了保证k、v和q的处理计算统一,kv使用了两次投影,为了保证稳定性,让query和kv不产生差异,query也做两次投影。2)可以节省模型的参数量。
\[\mathbf{c}_t^Q=W^{DQ}\mathbf{h}_t\]
\[[\mathbf{q}_{t,1}^C;\mathbf{q}_{t,2}^C;…;\mathbf{q}_{t,n_h}^C]=\mathbf{q}_t^C=W^{UQ}\mathbf{c}_t^Q\]
其中\(W^{D\bar{Q}}\in\mathbb{R}^{d_c^{\prime}\times d},W^{UQ}\in\mathbb{R}^{d_hn_h\times d_c^{\prime}},d_c^{\prime}=1536\)
3.2.3.5 Q、K增加位置编码
并没有像通常一样在\(q_{t}^{C},k_{t}^{C}\)的基础上乘上RoPE的矩阵,而是解耦,单独计算\(q_{t}^{C},k_{t}^{C}\)的位置编码并concat在后面。
Key:
\[\begin{aligned}
\mathbf{k}_t^R & =\mathrm{RoPE}(W^{KR}\mathbf{h}_t), \\
\mathbf{k}_{t,i} & =[\mathbf{k}_{t,i}^C;\mathbf{k}_t^R],
\end{aligned}\]
其中\(W^{KR}\in\mathbb{R}^{d_h^R\times d}\),实际中,\(d_h^R=d_h/2=64\)。并且,从上面式子可以看出来,其实\(\mathbf{k}_t^R\)是一个MQA的计算方式,即所有Head里的\(\mathbf{k}_{t,i}^C\)共享同一个\(\mathbf{k}_t^R\),即在每一个\(\mathbf{k}_{t,i}^C\)都concat同一个\(\mathbf{k}_t^R\),下标i是attention head的索引。
Query:
\begin{equation}\begin{cases}
[\mathbf{q}_{t,1}^R;\mathbf{q}_{t,2}^R;…;\mathbf{q}_{t,n_h}^R] & =\mathbf{q}_t^R=\mathrm{RoPE}(W^{QR}\mathbf{c}_t^Q), \\
\mathbf{q}_{t,i} & =[\mathbf{q}_{t,i}^C;\mathbf{q}_{t,i}^R],
\end{cases}\end{equation}
其中,\(W^{QR}\in\mathbb{R}^{d_h^Rn_h\times d_c^{\prime}}\)。和Key的位置编码计算不同的是,Query每个头里的编码是不一样的,每个头的\(\mathbf{q}_{t,i}^C\)后面concat的位置编码向量都不一样,是一种MHA的方式。
3.2.3.6 为什么要通过在Q、K的后面添加位置编码向量,而不是直接用RoPE变换矩阵和Q、K相乘?
先讲一下矩阵吸收运算
假设有两个向量\(x_1,x_2\in R^{3\times1}\),和两个变换矩阵\(P\mathrm{,}Q\in R^{2\times3}\)
方式一:常规计算
\[\begin{aligned}
x_1^{^{\prime}} & =Px_1 \\
x_2^{^{\prime}} & =Qx_2 \\
x_1^{^{\prime}T}x_2^{^{\prime}} & =(Px_1)^T*(Qx_2)=x_1^TP^TQx_2
\end{aligned}\]
方式二:矩阵吸收计算
\[Q^{^{\prime}}=P^TQ\]
\[x_2^{^{\prime\prime}}=Q^{^{\prime}}x_2\]
\[x_1^Tx_2^{^{\prime\prime}}=x_1^TQ^{^{\prime}}x_2=x_1^TP^TQx_2=x_1^{^{\prime}T}x_2^{^{\prime}}\]
通过上面的例子我们可以看到,两种方法计算出的结果是一样的,但第二种方法是先做了矩阵乘法,相当于把\(x_1\)的变换矩阵\(P\)吸收到了\(x_2\)的变换矩阵\(Q\)里。
a) 不加RoPE
如果不加RoPE,对qk进行计算:
\[q_{t,i}^T\times k_{j,i}=(W_{(i)}^{UQ}c_t^Q)^T\times W_{(i)}^{UK}c_j^{KV}=(c_t^Q)^T\times(W_{(i)}^{UQ})^TW_{(i)}^{UK}\times c_j^{KV}\]
不加RoPE,我们可以提前计算好\((W_{(i)}^{UQ})^TW_{(i)}^{UK}\),也就是两个变换矩阵互相吸收了。
b) 假设加入RoPE变换矩阵
\[q_{t,i}^T\times k_{j,i}=(\mathcal{R}_tW_{(i)}^{UQ}c_t^Q)^T\times\mathcal{R}_jW_{(i)}^{UK}c_j^{KV}=(c_t^Q)^T\times(W_{(i)}^{UQ})^T\mathcal{R}_t^T\mathcal{R}_jW_{(i)}^{UK}\times c_j^{KV}=(c_t^Q)^T\times(W_{(i)}^{UQ})^T\mathcal{R}_{t-j}W_{(i)}^{UK}\times c_j^{KV}\]
中间这个分量\((W_{(i)}^{UQ})^T\mathcal{R}_{t-j}W_{(i)}^{UK}\)是会随着t,j变化的,并不是个固定的矩阵,因此并不能提前计算好。所以论文中说RoPE与低秩变换不兼容。
c) 通过给q,k增加一个很小的分量,引入RoPE
\[q_{t,i}^T\times k_{j,i}=[q_{t,i}^C;q_{t,i}^R]^T\times[k_{j,i}^C;k_t^R]=q_{t,i}^Ck_{j,i}^C+q_{t,i}^Rk_t^R\]
所以最终q,k向量通过两部分拼接而成,计算权重时,由前后两部分分别相乘再相加得到。
前一项\(q_{t,i}^Ck_{j,i}^C\)是按照矩阵吸收的形式计算,后一项\(q_{t,i}^Rk_t^R\)按照MQA的方式计算,因为一个所有head公用同一个key的RoPE向量。
通过类似的计算方式,我们可以可以把v的上采样矩阵\(W_{UV}\)吸收到output的投影矩阵\(W_O\)中,
那为什么采用原始的RoPE不行吗,为什么非得让RoPE也吸收到矩阵运算呢?我们这里放到下一部分解答
3.2.3.7 进行MLA都要存储什么?
首先是KV Cache部分:
- \(c_t^{KV}\):位置t的token的kv的低秩表示,\(4\times d_h=512\)
- \(k_t^{R}\):位置t的token的RoPE向量,\(d_h / 2=64\),其在所有头共享。
其次是模型参数部分:
- qkv的下采样矩阵\(W^{DKV}\)和\(W^{DQ}\):用于把\(h_t\)投影到低维表示。
- 上采样矩阵\(W^{UK},W^{UV},W^{UQ}\)需要存储吗?其实不用,因为他们在矩阵运算中已经被吸收了,\(W^{UK},W^{UQ}\),两者进行了吸收,\(W^{O},W^{UV}\)两者进行了吸收,我们只需要保存吸收了的矩阵即可,这样大大节省了模型参数,我们以\(W^{UK},W^{UQ}\)为例,这两个矩阵的参数量分别为\(d \times d_c, d \times d_c^{\prime}\),吸收之后,两者形成的矩阵大小为\(d_c^{\prime} \times d_c\),因为\(d\)很大,而\(d_c, d_c^{\prime}\)很小,这样就大大减少了参数量。这种吸收的方式得益于将RoPE解耦,也就是用单独的一段向量表示位置编码,如果使用原始的RoPE变换,那么上述这些矩阵就无法吸收,也就无法节约参数,这也就回答了为什么非得让RoPE吸收到矩阵运算中去了,是为了节约存储的考虑,但是呢,这种方法也有弊端,让原本的乘性位置编码变成加性了,可能会降低性能。
- \(W^{KR},W^{QR}\)也不用存储了,因为他俩也可以吸收到矩阵运算中,只需要存储一个矩阵即可。