论文地址:Frequency-aware Feature Fusion for Dense Image Prediction
1 introduction
先说论文中几个名词:
- intra-category & inter-category similarity:会计算给定图片每个类的一个category center,就是某个类所有feature vector的一个均值,intra就是计算某个feature vector和其同类的category center的余弦相似度,inter就是计算和它不同类的category center的余弦相似度
- similarity margin:是第一条中intra和inter的差值。很明显,我们肯定希望一个feature vector的similarity margin越大越好,也就是和自己类的相似度尽可能高,和别的类尽可能低。
本文主要是提出了一种新的上(下)采样的方法,用于不同层级间的特征融合。作者认为普通的feature fusion会带来两个问题,一个是intra-category inconsistency,比如一个车子可能有不同的部分组成,车窗和车的轮胎在像素表现上有很明显的不同,故它们对应的feature vector可能会有较大差异(intra-category similarity很低),但是它们应该被预测到同一类别,因为它们都是属于车子的,这就是intra-category inconsistency,普通的线性插值上采样就会恶化这种现象,比如整个车子可能只有几个像素它们的intra-category similarity很低,但是使用线性插值之后,相似度低的像素就会更多;还有一个问题是boundary displacement,就是说普通的插值手段通常会过度的smooth,会导致边缘不明显,出现边界位移的现象。
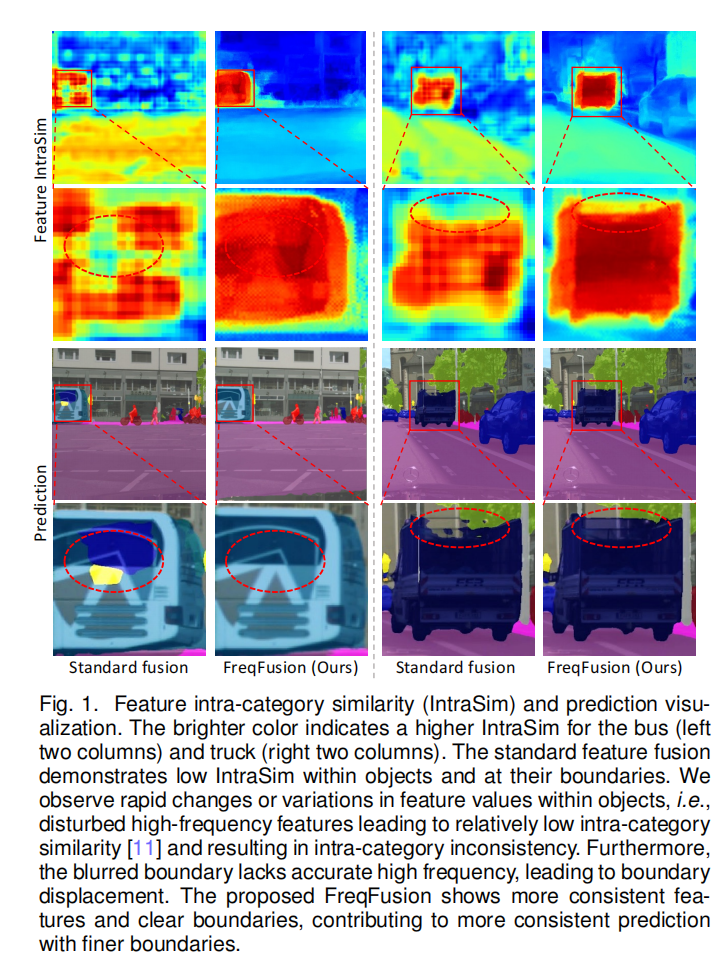
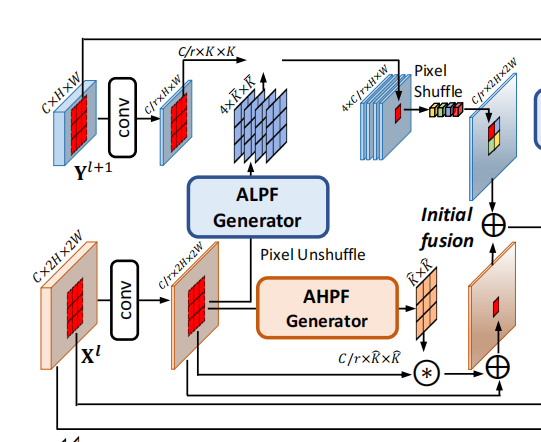
作者为了解决这个问题,提出了三种解决措施,Adaptive Low-Pass Filter (ALPF),offset generator,Adaptive High-Pass Filter (AHPF)。ALPF是创造一个低通low-pass的过滤器来减少由upsample带来的物体内的inconsistency,并进行平滑。offset generator 是通过计算位移来用具有高intra-category similarity的featurevector来resample和replace那些和周围像素具有低intra-category similarity的像素,这样同时能优化边界和内部区域。AHPF是为了提取恢复那些在经过downsampling之后丢掉的那些高频边缘特征。
offset generator和ALPF的目的好像差不多,都是为了减少inconsistency,对于ALPF,如果kernel size太大,有利于大块的inconsistent features,但是导致一些边缘细节被过度平滑;如果kernel size太小,有利于边缘和一些细小区域但是对于大片区域的inconsistent不能做出有效修正。基于此,作者提出了offset generator,因为作者观察到低intra相似度的区域周围极大概率会有一些高intra相似度的邻居,作者会计算局部的相似度并计算高相似度方向上的偏移量。因此,偏移发生器可以纠正大区域和薄边界区域中不一致的特征。
2 Method-Frequency-Aware Feature Fusion
2.1 Standard feature fusion Vs FreqFusion
2.1.1 Standard feature fusion:
\[\mathbf{Y}^l=\mathcal{F}^{\mathrm{UP}}(\mathbf{Y}^{l+1})+\mathbf{X}^l,\]
标准融合在纠正不一致的特征方面表现不足,其中简单的插值甚至可能将一个不一致的特征升级到多个不一致的像素,从而使问题恶化。此外,简单插值的输出往往倾向于过度平滑,导致边界位移。此外,lower level中的特征中的详细边界信息没有得到充分利用。
2.1.2 FreqFusion:
\[\begin{aligned}\mathbf{Y}_{i,j}^{l}&=\tilde{\mathbf{Y}}_{i+u,j+v}^{l+1}+\tilde{\mathbf{X}}_{i,j}^{l},\\\tilde{\mathbf{Y}}^{l+1}&=\mathcal{F}^{\mathrm{UP}}(\mathcal{F}^{\mathrm{LP}}(\mathbf{Y}^{l+1})),\quad\tilde{\mathbf{X}}^{l}=\mathcal{F}^{\mathrm{HP}}(\mathbf{X}^{l})+\mathbf{X}^{l}.\end{aligned}\]
示意图如下:
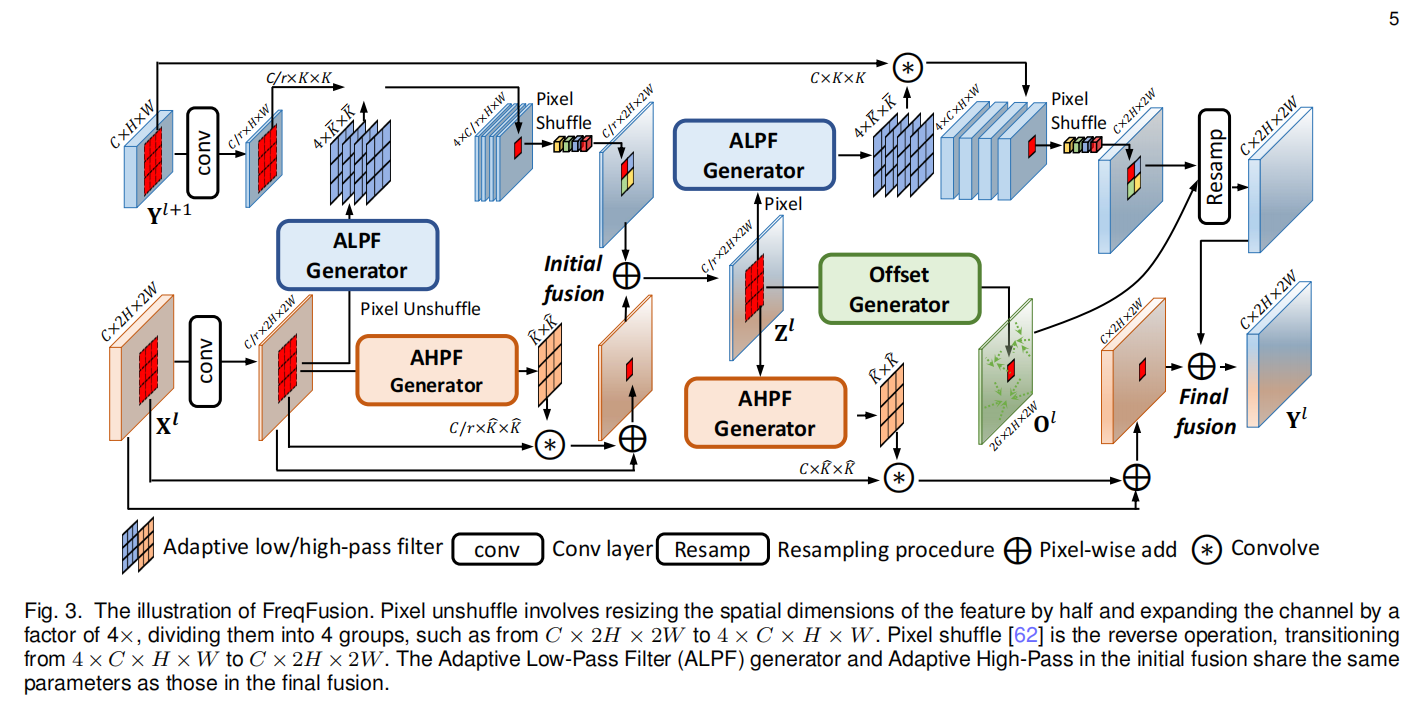
2.2 FreqFusion-Initial Fusion
Initial Fusion的的目的是压缩\(\mathbf{X}^{l}\)和\(\mathbf{Y}^{l+1}\),送进三个generator。普通的initial fusion通常是:
\[\mathbf{Z}^l=\mathcal{F}^\mathrm{UP}(\mathrm{Conv}_{1\times1}(\mathbf{Y}^{l+1})))+\mathrm{Conv}_{1\times1}(\mathbf{X}^l).\]
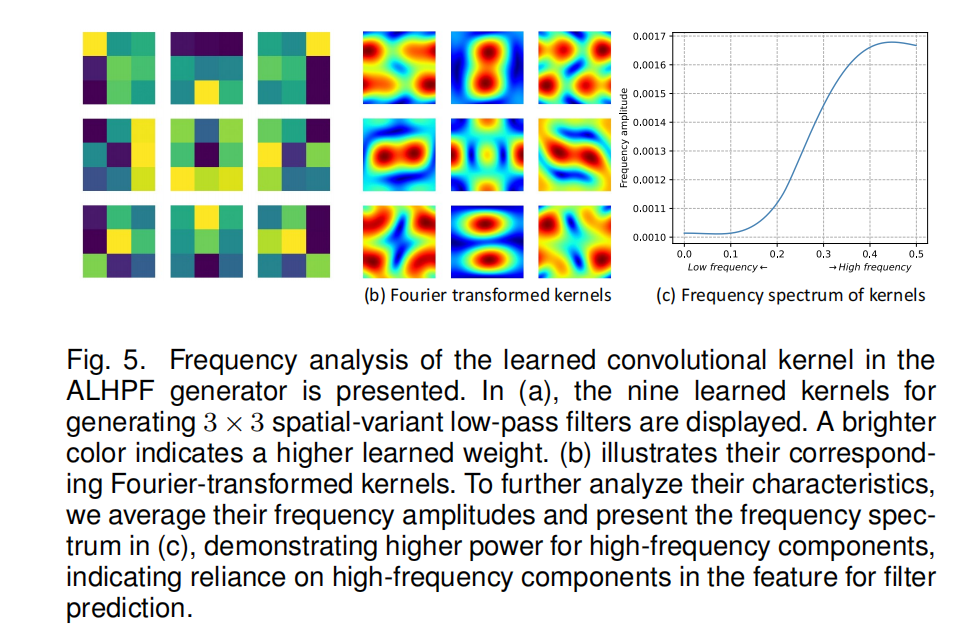
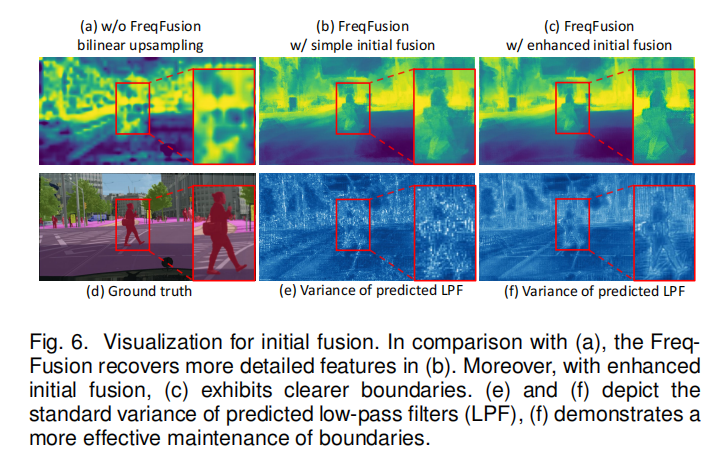
但是传统的initial fusion是有弊端的,简单线性插值的上采样会导致迷糊的边界;并且,ALPF会很依赖压缩特征中的高频信息(如fig.5),但是传统的卷积只能捕捉高频中的固定模式。
Enhanced Initial Fusion
作者首先对高分辨率的低等级特征做ALPF产生low-pass filter,用来upsample低分辨率的高等级特征。这一步的目的是借助高分辨率的特征信息来帮助低分辨率进行上采样。根据fig.5可以看出,ALPF非常依赖于compressed feature里的高频信息,但是卷积只能捕捉到固定模式的高频信息,因此,作者还使用了AHPF去提取高频特征,与具有固定学习权值的卷积不同,AHPF发生器所使用的空间变异高通滤波器显示了捕获高频模式的自适应能力,并且,AHPF还可以丰富特征中高频细节的表示。
2.3 FreqFusion-ALPF, Offset generator, AHPF
2.3.1 Adaptive Low-Pass Filter Generator
ALPF是用来预测动态低通滤波器的,用来平滑特征从而减轻feature inconsistency,从而更顺利地upsample low-level features。为了实现高质量的自适应低通滤波器,同时利用高级和低级特性的优点是至关重要的。ALPF使用initial fusion产生的compressed features \(\mathbf{Z}^{l}\)作为input去产生低通滤波器,具体过程如下:
\[\begin{aligned}
\bar{\mathbf{v}}^{l}& =\mathrm{Conv}_{3\times3}(\mathbf{Z}^{l}), \\
\mathbf{\bar{W}}_{i,j}^{l,p,q}& =\mathrm{Softmax}(\bar{\mathbf{V}}_{i,j}^{l})=\frac{\exp(\bar{\mathbf{V}}_{i,j}^{l,p,q})}{\sum_{p,q\in\Omega}\exp(\bar{\mathbf{V}}_{i,j}^{l,p,q})},
\end{aligned}\]
\(\bar{\mathbf{V}}^{l} \in \mathbb{R}^{\bar{K}^{2}\times2H\times2W}\)代表滤波器的权重,\(\bar{K}\)是kernel size,也就是说,每个像素点都会有一个kernel与之对应。然后会对\(\bar{\mathbf{V}}^{l} \)的每个通道进行softmax,这一操作就相当于一个平滑操作,把kernel进行平滑,创造一个low-pass filter。
接下来将\(\bar{\mathbf{W}}^{l}\)的H、W都减半,然后通道扩大4倍,然后将其分成四组,每组即为\(\mathbf{\bar{W}}^{l,g}\in\mathbb{R}^{\vec{K}^{2}\times H\times\bar{W}},\mathrm{~where~}g\in\{1,2,3,4\}\)代表group。然后进行如下操作:
\[\begin{aligned}
\tilde{\mathbf{Y}}_{i,j}^{l+1,g}& =\sum_{p,q\in\Omega}\bar{\mathbf{W}}_{i,j}^{l,g,p,q}\cdot\mathbf{Y}_{i+p,j+q}^{l+1}, \\
\mathbf{\tilde{Y}}^{l+1}& =\mathrm{PixelShuffle}(\mathbf{\tilde{Y}}^{l+1,1},\mathbf{\tilde{Y}}^{l+1,2},\mathbf{\tilde{Y}}^{l+1,3},\mathbf{\tilde{Y}}^{l+1,4}).
\end{aligned}\]
上述中的第一个公式就是对\(\mathbf{Y}^{l+1,g} \in {\mathbb{R}^{C\times H\times W}}\)使用四组权重分别进行四次“卷积”,不过这次的卷积不太一样,普通的卷积核的尺寸应该是\(K \times K \times C\),也就是每个通道都会有一个\(K \times K\)的权重,但是作者这里使用的是\(K^2\times H\times W\),也就是同一位置的不同通道公用一套权重,但是每个像素位置都有一个权重,这里就体现了“spatially variant”,也就是随着空间位置不同,权重也会不同,从而针对不同位置都可以捕获属于这个位置的独特信息,而不是像传统卷积一样,对于空间的每个位置使用同一套参数,不具有针对性。
上述中的第二个公式是接着第一个公式。我们使用四组权重处理完之后,会得到四个\(\tilde{\mathbf{Y}}^{l+1,g} \in {\mathbb{R}^{C\times H\times W}}\),然后使用PixelShuffle,将每一个像素划为\(2 \times 2\)份,由对应特征图的\(2^2\)个像素组成一个新的像素,从而进行上采样,即\([H,W,C\cdot r^2]>>>[H\cdot r,W\cdot r,C]\)
总体来说,就是先用卷积计算每个像素位置处的kernel weights,然后将权重smooth(softmax),然后将权重的channel扩张四倍,切分为四组,然后用这些spatially variant的权重去卷积原图,得到四张卷积之后的原图,然后用pixel shuffle组合起来。相比于普通的线性插值,这种上采样实现了从大到小(第一次卷积得到kernel weights)再到大(使用pixel shuffle)的过程,其每一个像素如何扩张,扩张成什么样子,是受其周围像素影响的,而不是像线性插值一样,仅仅由公式决定,相当于给上采样提供了一个感受野,每一个像素扩张成什么样子的四个像素,是由其周围像素决定,从而缓解了feature inconsistency的问题,缓解了是同一类像素但是similarity过低的问题。
2.3.2 Offset Generator
ALPF的kernel size大或者小都会有局限性,为了解决局限性,作者提出offset generator,因为低相似度的特征周围往往有高相似度的特征,所以作者想用高相似度的特征去替换低相似度的特征(sample towards features with high intra-category similarity),首先,计算local cosine similarity(周围八个像素):
\[\mathbf{S}_{i,j}^{l,p,q}=\frac{\sum_{c=1}^{C}\mathbf{Z}_{c,i,j}^{l}\cdot\mathbf{Z}_{c,i+p,j+q}^{l}}{\sqrt{\sum_{c=1}^{C}(\mathbf{Z}_{c,i,j}^{l})^{2}}\sqrt{\sum_{c=1}^{C}(\mathbf{Z}_{c,i+p,j+q}^{l})^{2}}}\]
然后会计算方向\(\mathrm{D}^l \in \mathbb{R}^{2G\times H\times W}\)和幅值\(\mathrm{A}^l \in \mathbb{R}^{2G\times H\times W}\):
\[\begin{aligned}
&\text{O} =\mathbf{D}^{l}\cdot\mathbf{A}^{l}, \\
&D^{l} =\mathrm{Conv}3\times3(\mathrm{Concat}(\mathbf{Z}^l,\mathbf{S}^l)), \\
&\text{A l} =\mathrm{Sigmoid}(\mathrm{Conv}3\times3(\mathrm{Concat}(\mathbf{Z}^l,\mathbf{S}^l))),
\end{aligned}\]
其中G代表offset的group数量。源代码中resample的方法是torch.nn.functional.grid_sample(),它是用坐标偏移量的方式来重新修整每个位置的像素
2.3.3 Adaptive High-Pass Filter Generator
根据采样定理(Nyquist-Shannon Sampling Theorem),在下采样中,频率大于下采样倍率的一半的信息会在下采样过程中丢失,因此作者设计AHPF来增强在采样中丢失的边界高频信息。
\[\begin{aligned}
\hat{\mathbf{v}}^{l}& =\mathrm{Conv}_{3\times3}(\mathbf{Z}^{l}), \\
\mathbf{\hat{W}}_{i,j}^{l,p,q}& =\mathbf{E}-\mathrm{Softmax}(\mathbf{\hat{V}}_{i,j}^{l}) \\
&=\mathbf{E}^{p,q}-\frac{\exp(\mathbf{\hat{V}}_{i,j}^{l,p,q})}{\sum_{p,q\in\Omega}\exp(\mathbf{\hat{V}}_{i,j}^{l,p,q})},
\end{aligned}\]
\(\mathbf{\hat{V}}^{l}\in\mathbb{R}^{\hat{K}^{2}\times H\times W}\)代表在每个位置的kernel weights;然后使用softmax平滑weights先得到low-pass filter,然后和单位矩阵做inversion操作,得到high-pass filter,然后add residually,来增强\(\mathrm{X}_{i,j}^l\)
\(\mathbf{\tilde{X}}_{i,j}^l=\mathbf{X}_{i,j}^l+\sum_{p,q\in\Omega}\mathbf{\hat{W}}_{i,j}^{l,p,q}\cdot\mathbf{X}_{i,j}^l.\)