现在大模型一般训练过程是pretrain->SFT->RLHF，现在大部分模型都是decoder-only，这里讲解也都是以decoder-only为例子。
第一阶段是pretrain的目的就是语言建模，让模型学会语言模式和知识，学会语言本身，它通常会使用规模很大的数据集，来自大规模网络文本（如 Wikipedia、Books、Common Crawl 等），它们不带标签，模型的输入和label是相同的（但要错开一位）。下一阶段是SFT，它的目的是训练一个更听话、更有用的对话助手，在pretrain阶段，模型学习到语言模式，但它不会回答用户的问题，通过SFT，在人工筛选的prompt-answer对上进行训练，让其学会回答用户的问题。最后一阶段是RLHF（Reinforcement Learning from Human Feedback），目的是训练一个更有礼貌、更有逻辑、更安全的模型。通过训练一个奖励模型，其能判断哪个回答更好，SFT之后的模型通过强化学习优化（PPO）引导模型产生奖励模型评分更高的回答。
1 训练
训练过程通过attention mask来实现自回归的并行训练，同时对输入和预测目标进行错位，这样就保证了decoder可以自回归地推理预测下一个词。
在训练过程中，模型接收输入序列，并尝试输出一个序列，其目标是与标签序列匹配。因此，对于输入序列中的每个token（例如，"This"），模型需要预测下一个token（在这个例子中是"is"）。
这种方法通过确保模型的每个预测（除了序列的开始）都有一个对应的正确答案（即标签），来促使模型学习如何根据当前的上下文预测下一个词。由于输入序列和标签序列在内容上是相同的，但在时间步骤上错开了一位，这样就实现了自回归模型训练过程中所需的对齐。
下面是pretrain阶段一个训练sample的例子
# 训练时target需要将input原始文本错开一位形成target目标文本，保证decoder可以通过BOS的信息预测出This # 输入tokens…… inputs = [BOS, "This", "is", "a", "sentence", "to", "translate", "."] # 错位的目标tokens，实现用 BOS -> This target = ["This", "is", "a", "sentence", "to", "translate", ".", EOS]
下面是SFT阶段一个训练sample的例子，就是instruction tuning
# 这里举的例子并没有BOS，因为Instruction tuning BOS不是很关键，就算有也不再BOS上计算loss，loss只在Assistant的生成上计算，但是EOS一定要有 # 这个例子里我只在最后面添加了EOS，有时候，在用户的提问后面也会添加EOS，并在这个位置上计算loss，让模型学习到哪里是用户提问的结束，在这里为了可读性我就没有写 # 输入tokens inputs = ['User', ':', ' 请', '将', '这', '段', '话', '翻', '译', '成', '英', '文', '：', '我', '喜', '欢', '机', '器', '学', '习', '。'\n','Assistant', ':', ' I', ' like', ' machine', ' learning', <STOP>] # 错位的目标tokens target = [':', ' 请', '将', '这', '段', '话', '翻', '译', '成', '英', '文', '：', '我', '喜', '欢', '机', '器', '学', '习', '。'\n','Assistant', ':', ' I', ' like', ' machine', ' learning', <STOP>]
注意：在实际训练的时候，input_ids和label并不需要手动错位，只需要将input_ids复制给一份赋给label即可，在 Hugging Face 的实现里，training 时已经实现好了偏移一位的逻辑，不需要我们再手动实现了。详见：Shifting ids to the right when training GPT-2 on text generation? – Beginners – Hugging Face Forums[2]
在训练时，采用的是causal attention，也就是看不见之前的token，因此，各个位置next token的预测是并行的，直接将整个input输入进去，然后直接在每个位置计算loss即可。
2 推理
在自回归生成过程中，每次生成的token（来自value的最后一个）都会被附加到原始输入序列之后，使得输入序列在每一步都会变长。这样就导致了 输出序列的长度 随着每个时间步的生成而递增。
3 LLM Padding细节
3.1 为什么要Padding？
当我们需要进行 batch 推理时，我们会涉及 padding 操作，这是因为 batch 中的句子长度不一，我们需要将句子 padding 到同样的长度以保证 LLM 可以并行处理。padding 操作涉及两个问题，一个是 padding 的策略，另一个是 padding 的位置（也就是 padding_side）。
3.2 padding策略是什么？
策略1:padding 到和句子中最长的句子一样长
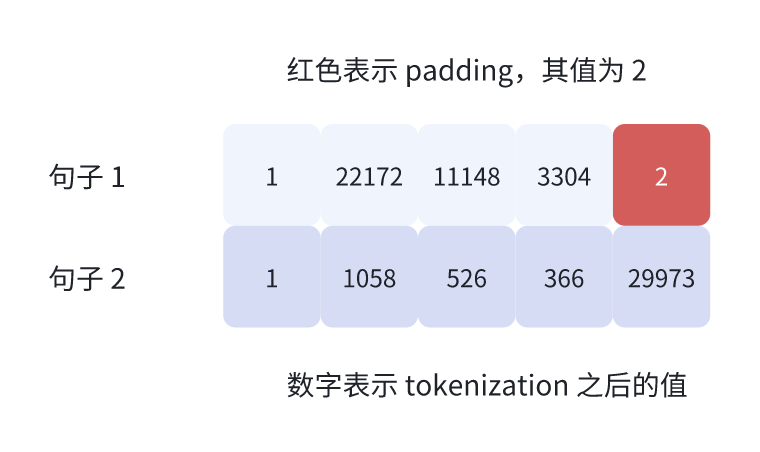
句子 1 原本有 3 个 token，句子 2 有 5 个 token，经 padding 后，句子 1 也有 5 个 token，其中最后两个是 pad token，它的值在这里是 2。
策略2:padding到指定长度
假设 padding 到长度 6，则 padding 后的结果如下图
通常是使用第一种策略，初始化 tokenizer 时设置 padding=True 或者 padding=’longest’ 即可。
3.3 padding_side是什么？
这个参数是用于指定padding到左边还是右边。huggingface的transformers的tokenizer默认是padding右边。LlamaTokenizer 没有对此进行修改，所以它同样默认是 padding 右边。而padding左边如下图：
那么，为什么 transformers 中的 LLama 或者大多数的 LLM 中，padding_side=’right’ 会导致结果不符合期望呢，接下来会具体介绍。
如果padding右边，可能会产生如下警告：A decoder-only architecture is being used, but right-padding was detected! For correct generation results, please set padding_side=’left’ when initializing the tokenizer.
3.4 padding_side的影响
谈到 padding，我们自然要考虑 attention_mask，借助 attention_mask 可以在计算 attention weight 时将 padding 带来的影响屏蔽掉。下面是设置不同的 padding_side，tokenizer 的输出：
没有设置 padding_side 或者 padding_side=’right’：
>>> from transformers import LlamaForCausalLM, LlamaTokenizer
>>> tokenizer = LlamaTokenizer.from_pretrained("meta-llama/Llama-2-7b-hf")
>>> tokenizer.pad_token = tokenizer.eos_token
>>> prompts = ["hello llama", "who are you?"]
>>> tokenizer(prompts, return_tensors="pt", padding=True)
{
'input_ids': tensor([[ 1, 22172, 11148, 3304, 2], [ 1, 1058, 526, 366, 29973]]),
'attention_mask': tensor([[1, 1, 1, 1, 0], [1, 1, 1, 1, 1]])
}
tokenization 后：
- “hello llama” 的 input_ids 为 [1, 22172, 11148, 3304, 2]，attention_mask 为 [1, 1, 1, 1, 0]，attention_mask 中的 0 表示 padding
- “who are you” 的 input_ids 为 [1, 1058, 526, 366, 29973]，attention_mask 为 [1, 1, 1, 1, 1]
设置 padding_side=’left’：
>>> from transformers import LlamaForCausalLM, LlamaTokenizer
>>> tokenizer = LlamaTokenizer.from_pretrained("meta-llama/Llama-2-7b-hf", padding_side="left")
>>> tokenizer.pad_token = tokenizer.eos_token
>>> prompts = ["hello llama", "who are you?"]
>>> tokenizer(prompts, return_tensors="pt", padding=True)
{
'input_ids': tensor([[ 2, 1, 22172, 11148, 3304], [ 1, 1058, 526, 366, 29973]]),
'attention_mask': tensor([[0, 1, 1, 1, 1], [1, 1, 1, 1, 1]])
}
tokenization 后：
- “hello llama” 的 input_ids 为 [2, 1, 22172, 11148, 3304]，attention_mask 为 [0, 1, 1, 1, 1]，attention_mask 中的 0 表示 padding
- “who are you” 的 input_ids 为 [1, 1058, 526, 366, 29973]，attention_mask 为 [1, 1, 1, 1, 1]
要理解 padding_side=’right’ 为什么会导致结果不正确，关键的点是 next token 的预测是使用句子的最后一个 token 经过 transformer 层之后输出的 logit 来得到 next token 的。下面是 model.generate通过多次跳转后来到 next token 的处理逻辑：
model_inputs = self.prepare_inputs_for_generation(input_ids, **model_kwargs) # forward pass to get next token outputs = self( **model_inputs, return_dict=True, output_attentions=output_attentions, output_hidden_states=output_hidden_states, ) next_token_logits = outputs.logits[:, -1, :] # argmax next_tokens = torch.argmax(next_tokens_scores, dim=-1)
从上面的代码可以看到，句子最后一个 token 所对应的 logit 会被用来计算 next token，因此，最后一个 token logit 的计算是否正确决定了推理的结果是否正确。
接下来，我们来看一下 padding_side=’left’ 和 padding_side=’right’，最后一个 token 所对应的 logit 是否是正确计算的。
我们先来看 padding_side=’left’ 的最后一个 logit 的计算过程，省略中间的具体细节，只给出关键的过程），这里只关注句子 “hello llama”：
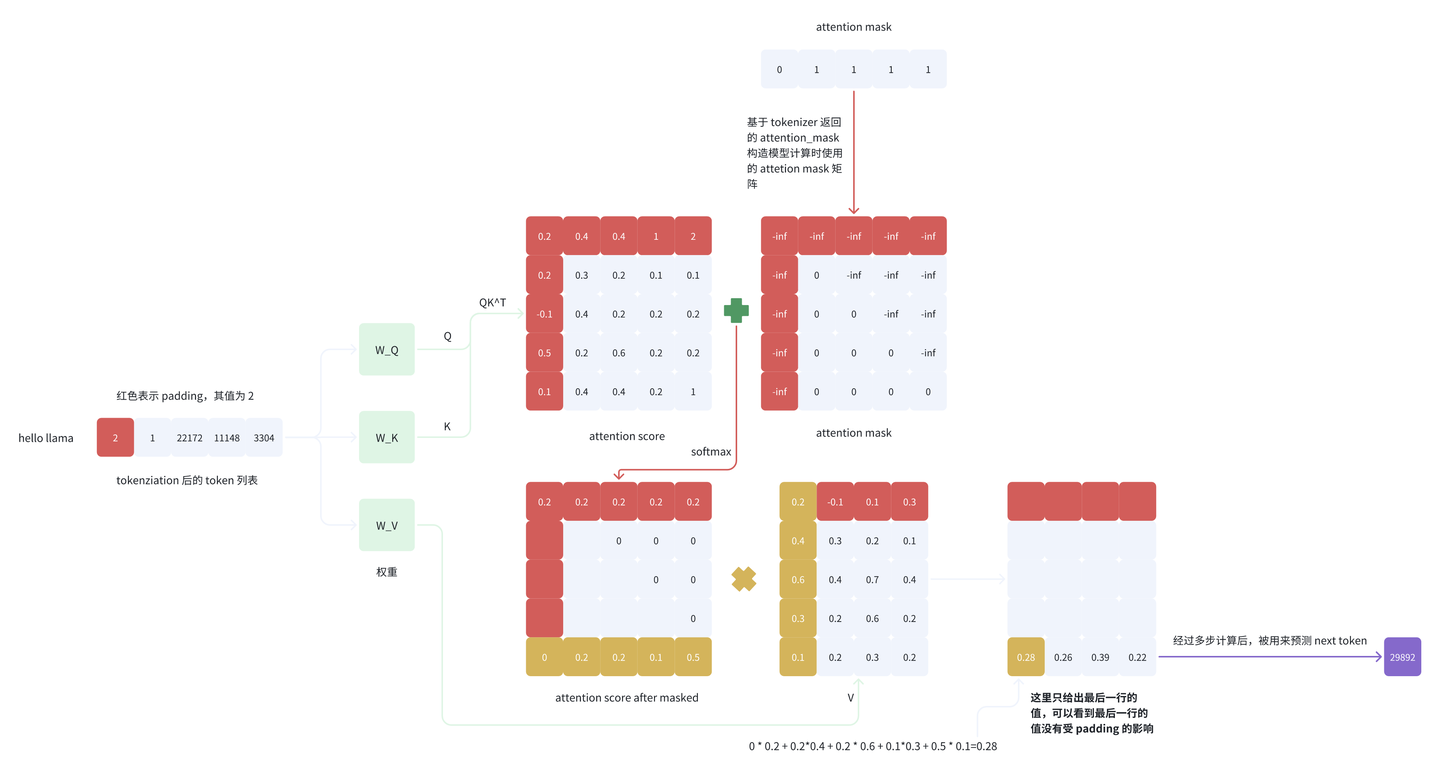
可以看到，attentionmap的最后一行的第一个值为0，在和value做矩阵乘法的时候，value的第一行（也就是padding token）始终会被屏蔽屏蔽掉，不参与最后一个token的计算。即最后一个 token 所对应的 logit 的计算没有受 padding 的影响，该 logit 的计算过程正确。
我们接下来看一下 padding_side=’right’ 的最后一个 logit 的计算过程：
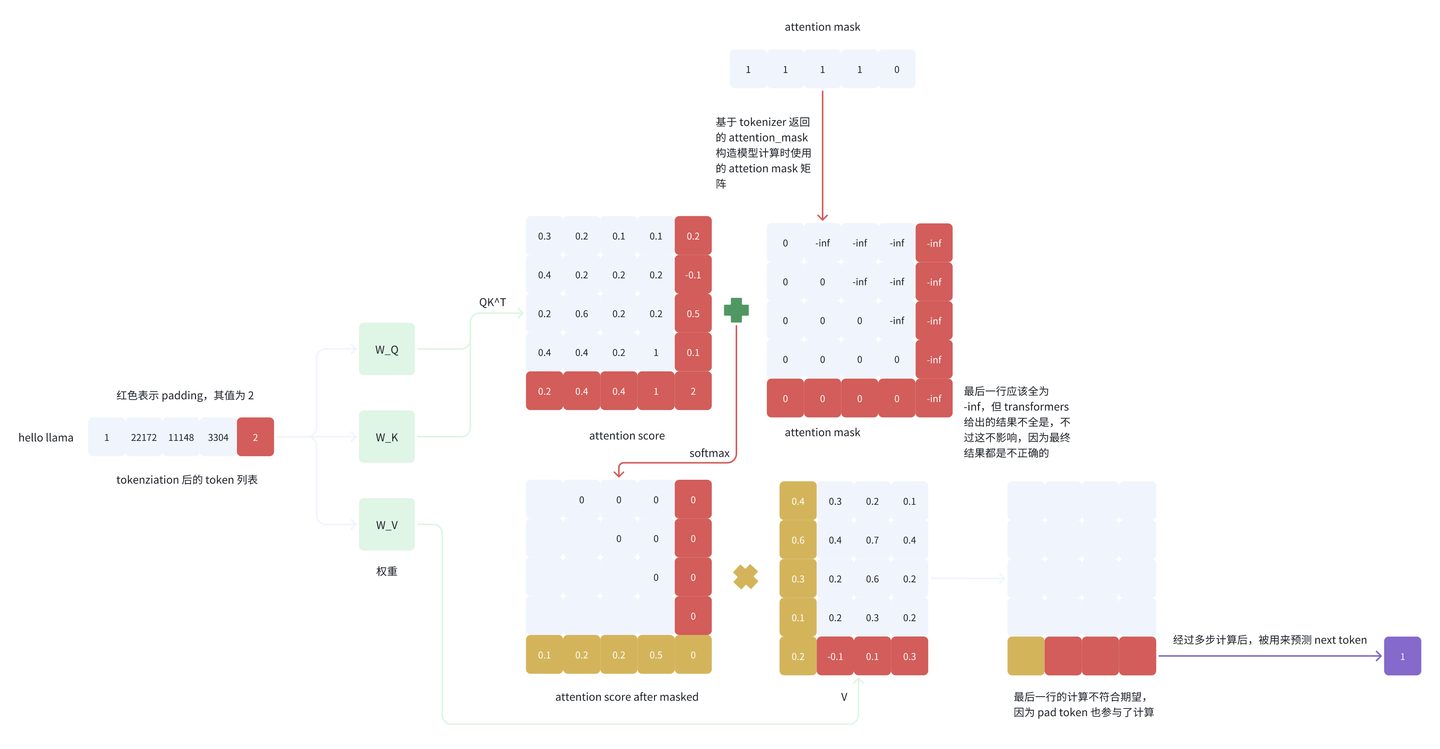
attention map的最后一行是由padding token和其他token计算得来的相似度，是没有用的，我们用这些相似度对value加权平均得到的最后一个token，必然也是错误的，即最后一个 token（pad token）所对应的 logit 的计算不正确，因为 pad token 也参与了计算，而且，attention map的最后一行是无用的信息，而正确预测 next token 的时候 pad token 是不应该参与计算的。
这时候有人会说：那我们使用最红计算结果的倒数第二个token作为改次预测的结果不行吗。理论上是可以的，但是，在上面的源码里，next token是取的最后一行的结果，这种取第二个token，理论上可行，但实际上和源代码实现相违背。
3.5 Llama 官方 batch 推理流程
Llama 中 batch 推理采用 padding 右边的做法，它首先创建一个大小为（bsz, total_len）值为 pad_id（值为 -1，表示无 padding token）的 tensor，其中 bsz 表示 batch size，total_len 表示模型的输入输出总长度。
total_len = min(params.max_seq_len, max_gen_len + max_prompt_len) pad_id = self.tokenizer.pad_id tokens = torch.full((bsz, total_len), pad_id, dtype=torch.long, device="cuda")
假设 bsz=2, total_len=5，则 tokens 为 [[-1, -1, -1, -1, -1], [-1, -1, -1, -1]]。
然后使用 prompt_tokens（输入）对其赋值，
for k, t in enumerate(prompt_tokens): tokens[k, : len(t)] = torch.tensor(t, dtype=torch.long, device="cuda")
假设 prompt_tokens 为 [[22172, 11148, 3304], [[1058, 526, 366, 29973]]，则 tokens 变成[[22172, 11148, 3304, -1, -1], [1058, 526, 366, 29973, -1]]。最后从 min_prompt_len 这个位置开始推理，对于的上面的 prompt_tokens，其 min_prompt_len 值为 3
prev_pos = 0
for cur_pos in range(min_prompt_len, total_len):
logits = self.model.forward(tokens[:, prev_pos:cur_pos], prev_pos)
if temperature > 0:
probs = torch.softmax(logits[:, -1] / temperature, dim=-1)
next_token = sample_top_p(probs, top_p)
else:
next_token = torch.argmax(logits[:, -1], dim=-1)
next_token = next_token.reshape(-1)
# only replace token if prompt has already been generated
next_token = torch.where(
input_text_mask[:, cur_pos], tokens[:, cur_pos], next_token
)
tokens[:, cur_pos] = next_token
for 循环第一次迭代时，cur_pos 等于 3，则把前三列 token [[22172, 11148, 3304], [[1058, 526, 366]]传给 model.forward 方法，假设该方法返回的 logits 经过 argmax 后得到第一个句子的 next token 为 29892，第二个句子的 next token 为 115，此时只更新第一个句子的 token，因为第二个句子还没真正开始预测。经过第一次迭代后，tokens 变成了 [[22172, 11148, 3304, 29892, -1], [1058, 526, 366, 29973, -1]]。最终经过多次迭代后，得到两个句子的最终预测结果。
可能会有如下问题：既然padding_side=’right’ 会产生不正确的结果，为什么Llama还是采用padding 右边的做法呢？
解答：在 transformers 中使用 padding right 会产生不正确的结果，而 Llama 中的 padding right 实际上是从最短句子的末位token开始batch处理的，也就是说，即便padding right，但是padding始终不参与计算，结果是正确的，只是不高效。
3.6 训练时怎么pad？
上文都在讲推理时怎么pad，那训练时呢？实际上，训练时一般不进行padd。为了提升训练效率（padding 相当于浪费了显存和做了无用的计算），训练的时候一般不 padding，大概的思路：假设 batch size = 2，max_seq_len = 16，sequence 1、2、3、4 分别有 7、9、6、10 个 token，那么就可以组成[[s1+s2], [s3+s4]] 进行训练，这个时候需要构造一个正确的 casual attention mask。
4 位置编码
4.1 为什么要使用位置编码？
之前的时序模型，比如RNN，是天然带有时间属性的，因为输入是一个一个输入进去的，但是Transformer不是，因为句子中的单词都是同时输入进模型中去，并且在做self-attention的时候，并没有考虑词的先后顺序。比如，对于两个句子：“我爱中国”，和“中国爱我”，我们看‘我’这个字，在两个句子中分别对应第0个位置和第3个位置，经过self-attention之后，如果没有位置编码，第0个位置的value和第3个位置的value是一样的，但很显然，它们的value应该不一样，因为在在句子中的位置不同，两个句子的意思也就不同。
4.2 Transformer原始架构位置编码-sin/cos编码
它是一种绝对位置编码，也就是每个位置有一个固定的向量。假设其某个向量维度为\(d_{model}\)，则对于位置在pos处的向量，其第2i和2i+1维度处的位置编码为：
\[PE_{(pos,2i)}=sin(pos/10000^{2i/d_{\mathrm{model}}})\\PE_{(pos,2i+1)}=cos(pos/10000^{2i/d_{\mathrm{model}}})\\i\in[0, d_{model}/2-1]\]
然后，在输入到模型之前，会在input embedding上加上上述position embedding，然后再输入到模型里。
但是这种编码有一些问题：
- 位置是绝对的，不可泛化：每个 position 都被编码成一个确定的向量；如果训练只见过最长为2048token数量的序列，那么模型完全不知道怎么处理 pos = 30000 的位置；模型没有外推能力
- 只能表示绝对位置，不能表达“相对距离”：这种绝对位置编码不具备“相对位移”的结构；比如：无法识别这两个token之间“相距5”意味着什么。所以模型无法学习重复结构，比如逗号前总是有形容词出现。
什么是模型外推能力？
外推性是指大模型在训练时和预测时的输入长度不一致，导致模型的泛化能力下降的问题。例如，如果一个模型在训练时只使用了512个 token 的文本，那么在预测时如果输入超过512个 token，模型可能无法正确处理。这就限制了大模型在处理长文本或多轮对话等任务时的效果。
4.3 RoPE
4.3.1 RoPE背景
RoPE是一种相对位置编码（但其实也是一种绝对位置编码，给每个位置的向量嵌入了位置信息，但在相乘运算计算内积的时候，实现了相对位置的建模）。RoPE希望通过位于m、n两个位置向量的点积，即\(f(q,m)\cdot f(qk, n)\)能带有相对位置信息m-n，因此建模目标可以表示为：找到一个函数\(g\)，使得下述式子成立：
\[f_q\left(x_m,m\right)\cdot f_k\left(x_n,n\right)=g(x_m,x_n,m-n)\]
4.3.2 理解RoPE
RoPE是乘性的，并且不是在输入到模型之前进行编码，而是在做self-attention之前对token进行位置编码，对于两个位置在m，n处的token \(x_m,x_n\)，其proj分别为\(W_q, W_k\)，这里直接给出它俩的编码公式：
\[x_m^{^{\prime}}=W_qx_me^{im\theta}=(W_qx_m)e^{im\theta}=q_me^{im\theta}\\x_n^{^{\prime}}=W_kx_ne^{in\theta}=(W_kx_n)e^{in\theta}=k_ne^{in\theta}\]
我们以\(x_m\)投影生成的\(q_m\)为例，假设词向量只有两个维度，则这个二维向量可以表示成虚数的形式，即\(q_m=q_m^1+\mathrm{i}q_m^2\)，则\(x_m^{^{\prime}}\)有：
\[\begin{aligned}
x_m^{^{\prime}}& =q_me^{\mathrm{i}m\theta}=(q_m^1+\mathrm{i}q_m^2)(cos(m\theta)+\mathrm{i}sin(m\theta)) \\
& =(q_m^1cos(m\theta)-q_m^2sin(m\theta))+\mathrm{i}(q_m^2cos(m\theta)+q_m^1sin(m\theta))
\end{aligned}\]
将其写为向量的形式，有：
\[[q_m^1cos(m\theta)-q_m^2sin(m\theta),q_m^2cos(m\theta)+q_m^1sin(m\theta)]\]
写成矩阵相乘的形式，即为（不难发现就是query向量乘上了一个旋转矩阵，让\(q_m^1，q_m^2\)绕原点旋转\(m\theta\)度）：
\[\begin{pmatrix}
cos(m\theta) & -sin(m\theta) \\
sin(m\theta) & cos(m\theta)
\end{pmatrix}
\begin{pmatrix}
q_m^1 \\
q_m^2
\end{pmatrix}\]
所以说，对于\(x_m^{^{\prime}}、x_n^{^{\prime}}\)，有：
\[\begin{gathered}
x_m^{^{\prime}}=
\begin{pmatrix}
cos(m\theta) & -sin(m\theta) \\
sin(m\theta) & cos(m\theta)
\end{pmatrix}
\begin{pmatrix}
q_m^1 \\
q_m^2
\end{pmatrix} \\
x_n^{^{\prime}}=
\begin{pmatrix}
cos(n\theta) & -sin(n\theta) \\
sin(n\theta) & cos(n\theta)
\end{pmatrix}
\begin{pmatrix}
k_n^1 \\
k_n^2
\end{pmatrix}
\end{gathered}\]
那这种公式为什么能够建模相对位置呢，我们将\(x_m,x_n\)做矩阵乘法（模拟在attention map里q和v运算过程，假设词向量只有两个维度）：
\[x_m^{^{\prime}T}x_n^{^{\prime}}=\left(q_m^1q_m^2\right)
\begin{pmatrix}
cos((m-n)\theta) & -sin((m-n)\theta) \\
sin((m-n)\theta) & cos((m-n)\theta)
\end{pmatrix}
\begin{pmatrix}
k_n^1 \\
k_n^2
\end{pmatrix}\]
因此，我们就找到了这个函数\(g\)，这个函数可以计算两个向量的点积，并且还能嵌入两个向量在矩阵中所处位置的差异，这个函数的入参为\(x_m，x_n，m-n\)：
\[\begin{aligned}
& g(\boldsymbol{x}_m,\boldsymbol{x}_n,m-n) \\
& =
\begin{pmatrix}
\boldsymbol{q}_m^{(1)} & \boldsymbol{q}_m^{(2)}
\end{pmatrix}
\begin{pmatrix}
\cos((m-n)\theta) & -\sin((m-n)\theta) \\
\sin((m-n)\theta) & \cos((m-n)\theta)
\end{pmatrix}
\begin{pmatrix}
k_n^{(1)} \\
k_n^{(2)}
\end{pmatrix}
\end{aligned}\]
从上式子可以看出，在做点积的时候，就已经考虑了两者之间位置的差异。
4.3.3 从二维拓展到多维
接着我们从二维扩展到多维上去，对于多维\(q_m\)，有：
\[\begin{pmatrix}
\cos m\theta_0 & -\sin m\theta_0 & 0 & 0 & \cdots & 0 & 0 \\
\sin m\theta_0 & \cos m\theta_0 & 0 & 0 & \cdots & 0 & 0 \\
0 & 0 & \cos m\theta_1 & -\sin m\theta_1 & \cdots & 0 & 0 \\
0 & 0 & \sin m\theta_1 & \cos m\theta_1 & \cdots & 0 & 0 \\
\vdots & \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\
0 & 0 & 0 & 0 & \cdots & \cos m\theta_{d/2-1} & -\sin m\theta_{d/2-1} \\
0 & 0 & 0 & 0 & \cdots & \sin m\theta_{d/2-1} & \cos m\theta_{d/2-1}
\end{pmatrix}
\begin{pmatrix}
q_0 \\
q_1 \\
q_2 \\
q_3 \\
\vdots \\
q_{d-2} \\
q_{d-1}
\end{pmatrix}\]
旋转矩阵是一个正交矩阵，只会旋转向量，而不会改变向量的模长，因此不会改变原来模型的稳定性。
因为旋转矩阵的稀疏性，通常以下面方式计算位置编码来节省算力：
\[\begin{pmatrix}
q_{0} \\
q_{1} \\
q_{2} \\
q_{3} \\
\vdots \\
q_{d-2} \\
q_{d-1}
\end{pmatrix}\otimes
\begin{pmatrix}
\cos m\theta_{0} \\
\cos m\theta_{0} \\
\cos m\theta_{1} \\
\cos m\theta_{1} \\
\vdots \\
\cos m\theta_{d/2-1} \\
\cos m\theta_{d/2-1}
\end{pmatrix}+
\begin{pmatrix}
-q_{1} \\
q_{0} \\
-q_{3} \\
q_{2} \\
\vdots \\
-q_{d-1} \\
q_{d-2}
\end{pmatrix}\otimes
\begin{pmatrix}
\sin m\theta_{0} \\
\sin m\theta_{0} \\
\sin m\theta_{1} \\
\sin m\theta_{1} \\
\vdots \\
\sin m\theta_{d/2-1} \\
\sin m\theta_{d/2-1}
\end{pmatrix}\]
4.3.4 RoPE的优势
sin编码是绝对位置编码，如果超出模型学习过的长度，模型就会失控，但是RoPE不一样，因为RoPE建模的是不同token之间位置的差别，所以RoPE有一定的外推性（注意是有一定的，但不多）。
比如模型在训练时max length为2048，但是在推理的时候，上下文长度来到了2060，虽然模型没有见过2060长度，但是由于RoPE编码，模型的能力是可以迁移的。比如对于2040和2050位置的两个token，尽管模型没见过这两个位置，但是模型见过2010和2020这两个token，这两对token的位置差是相同的，因此它们之间的attention是一致的，可以迁移的，因此RoPE在没见过的上下文长度下退化更慢。
但是呢，RoPE依然不能解决外推问题，当推理时上下文长度严重超过模型学习的长度的时候，会发生失控，比如训练时只有2048，但推理时来到10005，以10000和10005号token为例，他俩之间的旋转差为\(5*\theta_i\)，模型是见过的，但是RoPE本质上还是一种绝对位置编码，我们单拎出10000号token来看，其在空间上旋转了\(10000 * \theta_i\)度，会造成该向量所包含的语义信息失真，模型没见过旋转这么剧烈的向量，对于高频特征（i比较小的时候）最为明显，当i为0时（对应于向量的第一维度和第二维度），其在空间中旋转了\(10000 * \theta_i = 10000\)度，已经在空间中转疯了，模型根本没见过转了怎么多圈的向量，因此会出现失控。