1 参数高效微调

以语言模型为例子，微调一个预训练模型权重\(\Phi_0\)到\(\Phi_0+\Delta\Phi\)（\(\Delta\)就是参数更新量），通过一下LM objective去训练：

\[\max_\Phi\sum_{(x,y)\in\mathcal{Z}}\sum_{t=1}^{|y|}\log\left(P_\Phi(y_t|x,y_{<t})\right)\]

对于每一个下游任务，都会学习一个参数增量，它的维度和原模型权重维度相等，这导致不仅训练过程时间长开销大，而且如果想同时部署一个模型在多个下游任务的不同实例，存储空间占用很大。所以作者提出LoRA，旨在用较少的参数来表示\(\Delta\Phi=\Delta\Phi(\Theta)\)，并且\(|\Theta|\ll|\Phi_0|\)。

其他的参数高效微调方法，比如说添加adapter layers，会带来额外的推理延迟；prefix tuning（为每一层 Transformer 添加一些“前缀向量”，像“提示词”一样，注入任务信息）会减少下游任务可用的token数量。但是作者的LoRA没有这种问题，不仅没有延迟，而且存储还很高效。

2 LoRA

2.1 Intrinsic Dimension

我们先思考两个问题：为何用数千的样本就能将一个数十亿参数的模型微调得比较好？为何大模型表现出很好的few-shot能力？

Aghajanyan的研究表明：预训练模型拥有极小的内在维度(instrisic dimension)，即存在一个极低维度的参数，微调它和在全参数空间中微调能起到相同的效果。所以作者认为，在微调的过程中，参数的更新也是低秩的。

2.2 Method

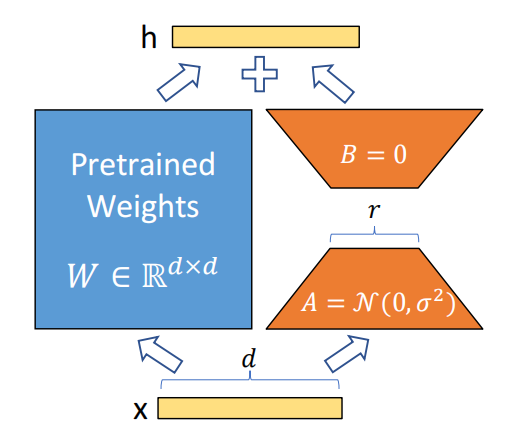
对于形状为\(W_{0}\in\mathbb{R}^{d\times k}\)的weight matrix，把它在微调时的参数更新表示为\(W_0+\Delta W=W_0+BA\)，其中\(B\in\mathbb{R}^{d\times r},A\in\mathbb{R}^{r\times k}\)，\(r\ll\min(d,k)\)，训练时只更新\(B,A\)，冻结\(W_0\)，模型经过该层的输出为：

\[h=W_0x+\Delta Wx=W_0x+BAx\]

2.3 Application of LoRA

LoRA可以用在任何神经网络的dense layers，在文中作者只应用在transformer里。transformer有4种权重矩阵，分别为\((W_q,W_k,W_v,W_o)\)，作者把\(W_q,W_k,W_v\)当作\(d_{model} \times d_{model}\)看待。作者对LoRA应该作用于哪个权重矩阵做出研究：

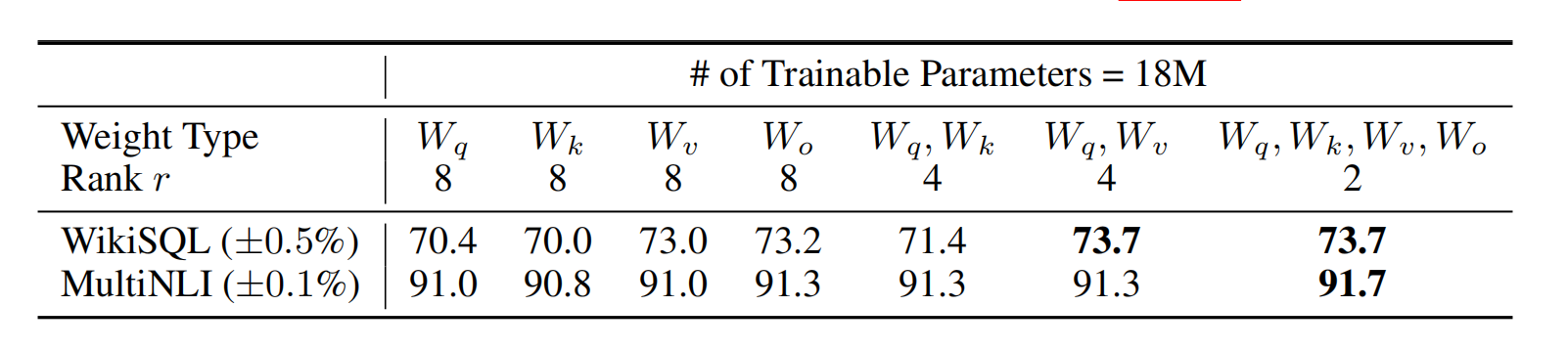
单单对q或者k进行adaption效果一般，同时对q、v的矩阵adapt效果最好；并且，由最后一列可以看出，相比于只使用单一类型的高秩adaption，使用更多低秩的效果会更好。

3 LoRA为什么在训练和推理的时候是高效的？

训练时：

因为相较于全参微调，使用LoRA微调，优化器不用存储那么多参数，只需要优化旁路即可。

举个例子，假设参数为1B，fp32下对应4G显存，优化器要存储梯度、一二阶动量。因此显存占用为4×4=16G

使用lora是之后，假如lora的参数只占了全参（x）的m%

• 参数部分（1+m）%x
• 梯度部分：m%x
• 优化器状态：2m%x

也就是说加起来为（1+4m%）x。当m=1%时，显存占用从4倍降低为1.04x。

推理时：

推理时，将A、B矩阵相乘，然后再和原投影矩阵相加，得到一个新的矩阵，这样不会带来任何额外的推理延迟。

4 题外话

多头注意力机制工程里是怎么实现的？

在transformer原论文里的图是：

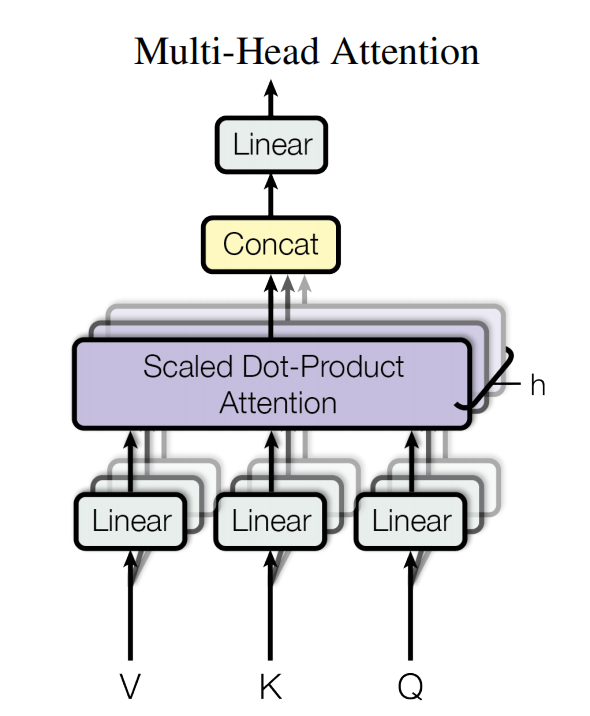
假设模型qkv的维度为\(d_{model}\)，每个head的维度为\(d_{head}\)（每个qkv在head里维度是一样的），一共有n个head，且有\(n \times d_{head} = d_{model}\)。接下来以query为例，可以从图上看出，每个head都有一个weight matrix \(W^{d_{model} \times d_{head}}\)把query从\(d_{model}\)投影到\(d_{head}\)，但是实际上在工程实现上，是把每一个head的\(W^{d_{model} \times d_{head}}\)合成一个大的矩阵\(W^{d_{model} \times d_{model}}\)，进行投影，然后把投影的结果进行分片，送入多个heads进行attention计算。