1 贝叶斯定理和全概率公式
1.1 全概率公式
假设\(A_1,A_2,\ldots,A_n\)是一个互斥且完备的划分(也就是样本空间被这些事件完全划分,没有重叠),那么有:
\[P(B)=\sum_{i=1}^nP(B|A_i)\cdot P(A_i)\]
也就是把“B 发生”的所有路径(通过不同的\(A_i\)发生)都考虑进去,再加权求和。
1.2 贝叶斯定理
贝叶斯定理描述了在已知某些先验条件下,如何更新事件的概率。它的核心思想是在获得新信息后更新原有信念。公式如下:
\[P(A|B)=\frac{P(B|A)\cdot P(A)}{P(B)}\]
举个例子:
某疾病的发病率为 1%(先验概率),检测这种病的测试准确率是 99%(即有病时检测为阳性的概率为0.99,无病时检测为阳性的概率为0.01)。如果某人检测为阳性,他实际上得病的概率是多少?
我们设A=得病,即\(P(A)=0.01\),B=检测为阳性,我们要求的是\(P(A|B)\)
现在已经有:\(P(B|A)=0.99, P(A)=0.01\),还需要求\(P(B)\),根据全概率公式,有:
\[P(B)=P(B|A)\cdot P(A)+P(B|\neg A)\cdot P(\neg A)=0.99\cdot0.01+0.01\cdot0.99=0.0198\]
将这些值代入贝叶斯定理公式,有:
\[P(A|B)=\frac{0.99\cdot0.01}{0.0198}\approx0.5\]
2 精确率、准确率、召回率、ROC和AUC值、PR曲线
二分类任务,1是正类,0是负类
- 类别实际为正,被分为负,则为FN
- 类别实际为正,被分为正,则为TP
- 类别实际为负,被分为负,则为TN
- 类别实际为负,被分为正,则为FP
2.1 各个指标
TPR(真阳性率)= TP / (TP + FN) 正类数据里被分类为正类的比例
FPR(假阳性率)= FP / (FP + TN) 负类数据里被分类为正类的比例
Precision(精确率、查准率)= TP / (TP + FP), 预测为正类的样本里,有多少是真的正类
Recall(召回率、查全率)= TP / (TP + FN),实际为正样本的样本里,有多少被预测出来了,和真阳性率(TPR)等价
F1-score:F1 = 2 * Precision * Recall / (Precision + Recall),平衡精确率和召回率的矛盾(比如提高召回率可能导致精确率下降),当两者都重要时,F1 是综合最优指标。
2.2 ROC曲线和AUC值
ROC曲线:以FPR为横轴,以TPR为纵轴,通过调整概率阈值绘制的曲线,曲线越靠近左上角,模型在 “控制误判(FPR)” 的同时 “识别正样本(TPR)” 的能力越强。
AUC值:ROC曲线下方的面积
- AUC=0.5:模型等同于随机猜测
- AUC<0.5:模型的能力还不如随机猜测
- AUC接近1:模型排序能力比较强,能够有效区分正负样本
AUC衡量模型对正负样本的相对排序能力,与样本比例无关,AUC 的值的物理意义是:随机取一个正样本和一个负样本,模型将正样本预测为 “更可能是正” 的概率,当AUC=1的时候,就是存在一个概率值,可以完美的区分所有正负样本。
AUC值对类别不平衡不敏感 —— 即使负样本占比极高,AUC 仍能反映模型对正负样本的区分能力(因为它关注的是 “相对排序” 而非 “绝对阈值”)。无论负样本有 100 个还是 10000 个,只要模型能在 “正样本 vs 任意负样本” 的比较中,正确给出更高的正样本概率,AUC 就会接近 1;
2.3 PR曲线和AP值
PR曲线:以Recall为横轴,Precision为纵轴,通过调整概率阈值绘制的曲线,曲线越靠近右上角,模型在 “查全少数类” 的同时 “保证预测精度” 的能力越强 —— 相比 ROC 曲线,PR 曲线更聚焦少数类的预测效果(ROC 曲线会受大量负样本的 TN 影响,PR 曲线则直接关注 TP、FP、FN)。
AP值:PR曲线下方的面积,综合衡量 PR 曲线的整体表现,AP 越高,模型对少数类(正类)的识别效果越好(尤其适合正样本极少量的场景,比如正样本占比 < 1%)。
2.4 当正负样本不均的时候,采用什么评价指标,不能用什么指标,为什么?
- 不能用精确率,TP / (TP + FP),当负样本特别多的时候,即便错判率很低,也会导致FP很大,导致分母很大,精确率被稀释,拉的很低。
- 可以用召回率,TP / (TP + FN),分母是正样本的总数,分子是被预测出来的正样本,和负样本没有关系,因此可以直接反映模型对正样本的捕捉能力。
- AUC与AP值:
- AUC的值和正负样本的数量量级差异没啥关系,衡量的是 “模型对正负样本的相对区分能力”,因此,正负样本不均的时候,可以用AUC值
- AP值是PR曲线下面的面积,PR曲线的纵轴是precision,当负样本特别多的时候,precision会很不稳定,PR 曲线的形状会随负样本数量急剧变化,甚至可能出现 “好模型的 PR 曲线反而不如差模型” 的错觉(因为 FP 绝对值太大)。而ROC里的FPR是比例,避免了这个问题
- 那么AP值对于正负样本不均的场景下,就没有作用了吗?其实不是的,AP值虽然会受负样本数量的影响,但和AUC相比,AP更具有针对性。负样本极多但需极致关注少数类(正样本)分类情况” 的场景下,比 ROC/AUC 更有针对性。
- 对于疾病判断这种,正样本比较少,负样本很多,并且误判的代价很大的情况下,也就是我们需要极致关注少数类别(发病)时,AP值是更好的,因为PR曲线很好的反映了模型误判和漏判的情况,值越高说明模型在 “少漏判” 和 “少误判” 之间做得越好,直接关联实际医疗决策的质量。
- 而对于其他场景下正负样本严重不均的情况下,比如电商商品推荐(错推了不感兴趣的商品,用户最多忽略,后果轻微),新闻分类(把体育新闻分到娱乐类,用户体验影响不大),这类任务中,核心是 “模型能不能把正负样本分开”,即正样本(用户感兴趣的商品 / 新闻)的预测概率是否显著高于负样本。即使正负样本比例不平衡(如感兴趣的商品只占 1%),只要模型的 “区分能力” 强(AUC 高),就能通过调整阈值满足需求(比如只推荐前 1% 高概率的商品)。ROC 曲线和 AUC 值直接衡量这种 “区分能力”,且不受样本比例影响,能稳定反映模型的核心性能 —— 此时 “漏判 / 误判的具体代价” 不重要,重要的是模型有没有能力把 “好的” 和 “不好的” 分开。
举个例子,假设任务是罕见病判断,一共有100个正样本(患者),100万个负样本(健康),
- 模型A:TP=90,FP=1000
- 模型B:TP=95,FP=10000
使用ROC/AUC判断:
- A:TPR=90/100=0.9,FPR=1000/100万=0.1%
- B:TPR=95/100=0.95,FPR=10000/100万=1%
使用AUC去判断的话,B模型会好,其TPR高了5%,而FPR略高了0.9%,AUC 值会略优于模型 A——ROC 会认为 “模型 B 更优”,因为它的 “相对区分能力” 更强(能多召回 5% 的患者)。
使用PR/AP值判断:
- A:P=90/(90+1000)=8.3%
- B:P=95/(95+10000)=0.94%
从PR曲线来说,P是纵轴,所以A的曲线会高于B,AP值也会明显优于B,所以从PR曲线来看,A模型更好,其实际决策质量更好,虽然其少召回了5%的病人,但是其大幅减少了健康人的误诊(10000->1000),避免过度治疗的医疗资源浪费和患者心理伤害。
总体来看,ROC/AUC,更注重的是比例,不关心负样本的绝对数量,ROC会认为,损失了0.9%的错判,但是带来了5%的召回,很值当,会让正负样本的排序能力更优,这完全是从比例来看的,并没有关心负样本的绝对数量,也就是说,并没有关心这0.9%的错判,实际代表多大的数字。
在这个例子当中,负样本一共有100万个,0.9%也就代表了9000人,可是这是疾病诊断,这9000人的绝对数量已经很大了,疾病的误判的代价很大,无论是从医疗资源开销的角度还是病人的心理角度来说;正因为PR曲线里的precision的计算时考虑了绝对数量,而不是比例,所以PR曲线才能将这9000人误判疾病的“代价”考虑进去,所以PR曲线更适合这种极致关注于少数类的场景,或者错判代价很大,正负样本严重不均的场景。
3 优化器
3.1 SGD(Stochastic Gradient Descent)随机梯度下降
SGD 是最基本的优化器,每次迭代用一个小批量数据(mini-batch)来估计梯度,然后更新参数。
\[\theta=\theta-\eta\cdot\nabla_\theta J(\theta)\]
简单、高效、易实现,内存开销小,适合大数据,但是对学习率敏感,不易调,容易震荡,收敛速度慢,不适合高维稀疏梯度或非平滑目标函数
那为什么是减去梯度呢?
函数某处的梯度就是函数在某处变化最快的方向,梯度(Gradient)是多元函数在某一点的 “变化率向量”,包含两个信息,一个是方向(函数在该点增长最快的方向),一个是大小(函数在这个增长最快的方向的变化率是多少)。
梯度的方向就是函数增长最快的方向,我们在机器学习里是想要最小化Loss,也就是让Loss变小,因此,我们需要让参数朝着让梯度的方向的反方向走,所以就是减去loss。
为什么用mini batch sgd,不用GD?
- GD计算成本太高,GD 每次更新参数都要计算整个数据集的梯度,非常慢。mini-batch 只需部分样本即可估计梯度,大大加快了每次更新的速度。
- 优化过程中“有噪声”,有助于逃离局部最优。损失函数肯定有很多局部最小值,如果使用全量GD,走到一个走到一个“坑”里后就不动了,因为所有样本的平均梯度在那点正好是 0。而使用mini batch SGD每次只随机看一小部分样本,是对真实梯度的随机近似,有一定的误差或者抖动,因此在靠近局部最优点的时候,梯度不会精确为0.
- 能与Batch Norm,Dropout等机制协同工作。
3.2 SGD Momentum
在使用SGD的时候,会有震荡问题,导致收敛变慢。
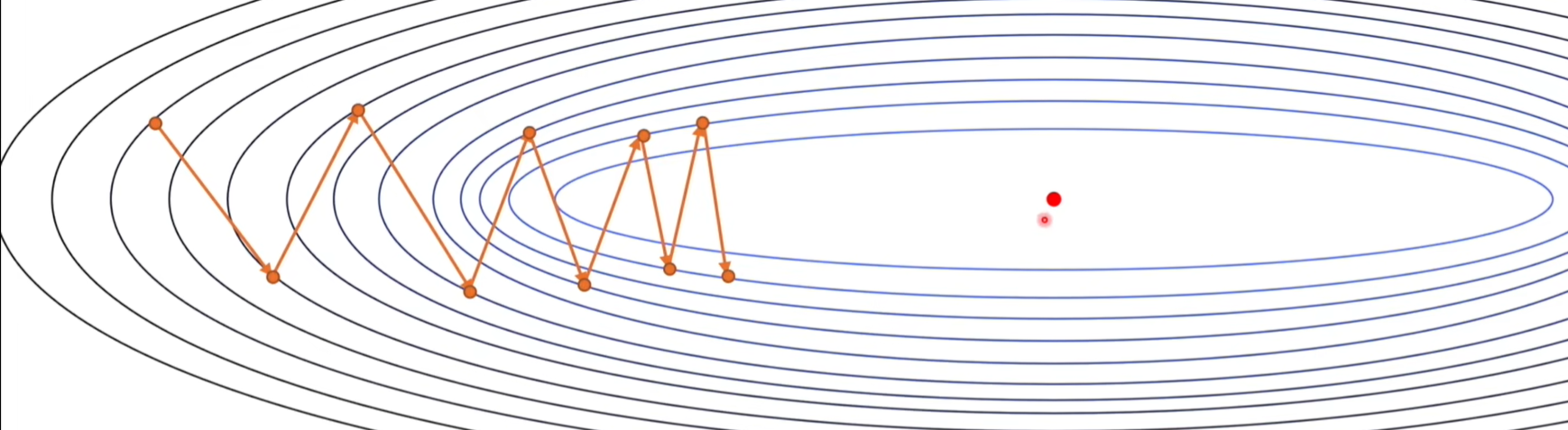
引入动量的好处是可以抵消梯度中那些变化剧烈的分量,如下图所示,如果我们每次都叠加历史梯度,那么它纵向上变化剧烈的梯度就可以被抵消,从而加快收敛速度。
\[\theta_{t+1}=\theta_t-\gamma v_t\]
\[v_t=\mu v_{t-1}+g_t\]
3.3 NAG
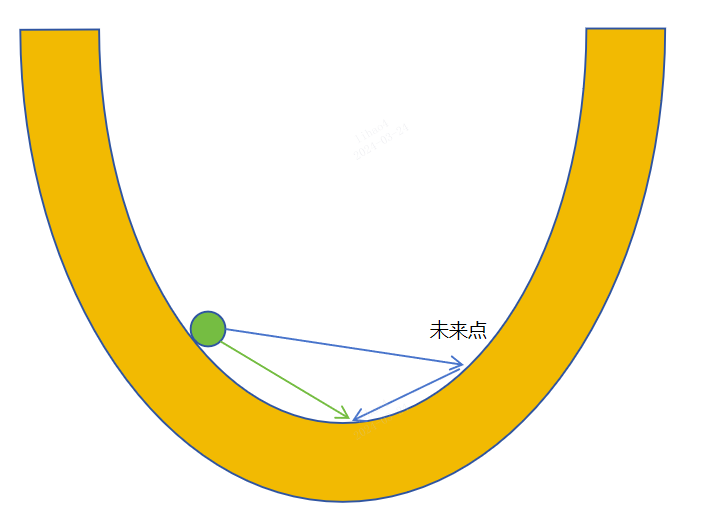
当优化接近最小值的时候,可能由于动量的存在,让参数冲过头,不会到达谷底,导致不停震荡,NAG就是为了解决这个问题,它的基本原理是在梯度更新之前往前看一步,让优化器可以预知未来的情况,从而对现在的梯度进行调整。通过这种方式,在接近最优解,Nesterov优化器比标准动量SGD算法有更快的收敛速度。因为这种“前瞻性”的操作能帮助优化器避免走得太远,就像是提前刹车,所以在接近最优解时更加稳定。公式为:
\[\theta_{t+1}=\theta_t-\gamma v_t\]
其中\(v_t=\mu v_{t-1}+g(\theta_t-\gamma\mu v_{t-1})\),这里的\(g(\theta_{t}-\gamma\mu v_{t-1})\)
3.4 AdaGrad
在前面提到的优化器中,我们还没有讲到学习率的问题。学习率代表了优化的步长,如果设定过大,可能会导致参数在最优点附近震荡,如果设置过小,则会导致模型收敛速度过慢。所以通常情况下我们会选择一种让学习率逐步减小的策略,例如余弦退火算法、StepLr策略等等。
但是即使是这样,我们还有一个问题没有解决,那就是不同参数应该有不同的学习率。
那是不是可以让模型自动地调整学习率呢?AdaGrad方法就可以实现这个愿望。公式:
\[\theta_{t+1}=\theta_t-\frac{\gamma}{\sqrt{s_t}+\varepsilon}g_t\]
其中\(s_t=s_{t-1}+g_t^2\),代表着历史中所有梯度的平方和。
这样做的好处是可以减小之前震荡过大的参数的学习率,增大更新速率较慢的参数的学习率,从而让模型可以更快收敛。
3.5 RMSProp
AdaGrad算法存在一个明显的问题,就是它要考虑所有的历史数据,这样就会导致\(s_t\)越来越大,学习率的分母变大了,也就会导致学习率越来越小,模型收敛的速度也就会变慢了。解决这个问题的方法还是采用指数加权移动平均法,减小更早的梯度对当前学习率的影响,而AdaGrad+指数加权移动平均法就是RMSProp方法了,其公式为:
\[\theta_{t+1}=\theta_{t}-\frac{\gamma}{\sqrt{s_{t}}+\varepsilon}g_{t}\]
其中,\(s_t=\alpha s_{t-1}+(1-\alpha)g_t^2\)代表着历史中所有梯度的平方和。
3.6 Adam
SGD momentum主要是优化梯度的方向,减少震荡,RMSProp是为每个参数都分配一个自适应学习率,那可不可以把两个方法结合起来呢?答案是可以!
Adam 结合了 Momentum(加速方向)和 RMSprop(自适应学习率),使用一阶矩(均值)和二阶矩(方差)的估计,自动调整每个参数的学习率,使用动量结合历史梯度信息,减少震荡。公式为:
\[\theta_{t+1}=\theta_t-\frac{\gamma}{\sqrt{s_t}+\varepsilon}v_t\]
其中,\(s_t=\beta_2s_{t-1}+(1-\beta_2)g_t^2\mathrm{;}v_t=\beta_1v_{t-1}+(1-\beta_1)g_t\)
adam里的一阶矩和二阶矩是什么?
- 一阶矩就是梯度的滑动平均,理解为梯度的期望,代表当前梯度的总体趋势,即为上述公式中的\(v_t\),用其代替原始梯度,避免剧烈震荡(像momentum一样)。
- 二阶矩就是梯度的平方的滑动平均,理解为梯度的方差估计,代表梯度的抖动程度,即为上述公式中的\(s_t\),它可以控制每个参数更新的步幅(像RMSProp一样)。
为什么梯度的平方的滑动平均,可以理解为梯度的方差估计?
在统计学中,对于变量\(g\),它的方差是:\(\mathrm{Var}(g)=\mathbb{E}[g^2]-(\mathbb{E}[g])^2\)。其中,第一项\(\mathbb{E}[g^2]\)我们使用梯度的指数移动平均去估计的,第二项\((\mathbb{E}[g])^2\),被忽略了,因为实际中,梯度的期望通常很小,所以\((\mathbb{E}[g])^2\)是一个数量级更小的值,可以忽略。因此可以简化的认为:
\[\mathrm{Var}(g)\approx\mathbb{E}[g^2]=s_t\]
我们使用动量除上梯度的平方的滑动平均,含义是:如果某个参数的梯度波动 大(\(s_t\) 大),就让它更新得慢(步子小);如果某个参数的梯度波动 小(\(s_t\) 小),就让它更新得快(步子大),从而让模型可以更快收敛。
3.7 AdamW
在AdamW提出之前,Adam算法已经被广泛应用于深度学习模型训练中。但是人们发现,理论上更优的Adam算法,有时表现并不如SGD momentum好,尤其是在模型泛化性上。
AdamW可以理解为加了l2正则化的adam
我们知道,L2范数(也叫权重衰减weight decay,注意有些时候l2正则化不一定就是weight decay,后面会讲)有助于提高模型的泛化性能。
但是AdamW的作者证明,Adam算法弱化了L2正则化的作用,所以导致了用Adam算法训练出来的模型泛化能力较弱。
这里讲一下是什么是l2正则化,什么又是weight decay,两者关系是什么样的?
1. 什么是l2正则化?
L2正则化的目的就是为了让权重衰减到更小的值,在一定程度上减少模型过拟合的问题,所以权重衰减也叫L2正则化。L2正则化就是在损失函数后面再加上一个正则化项:
\[C=C_0+\frac{\lambda}{2n}\sum_ww^2\]
其中C0代表原始的代价函数,后面那一项就是L2正则化项,它是这样来的:所有参数w的平方的和,除以训练集的样本大小n。λ就是正则项系数,权衡正则项与C0项的比重。另外还有一个系数1/2,1/2经常会看到,主要是为了后面求导的结果方便,后面那一项求导会产生一个2,与1/2相乘刚好凑整为1。系数\(\lambda\)就是权重衰减系数。
那为什么l2正则化可以实现权重衰减?
我们对参数\(w,b\)求偏导,会有:
\[\begin{aligned}
& \frac{\partial C}{\partial w}=\frac{\partial C_0}{\partial w}+\frac{\lambda}{n}w \\
& \frac{\partial C}{\partial b}=\frac{\partial C_0}{\partial b}.
\end{aligned}\]可以发现L2正则化项对b的更新没有影响,但是对于w的更新有影响:
\[\begin{aligned}
w & \to w-\eta\frac{\partial C_0}{\partial w}-\frac{\eta\lambda}{n}w \\
& =\left(1-\frac{\eta\lambda}{n}\right)w-\eta\frac{\partial C_0}{\partial w}.
\end{aligned}\]在不使用L2正则化时,求导结果中\(w\)前系数为1,使用正则化之后,系数小于1,它的效果是减小\(w\),减少过拟合,增强泛化性,这也就是权重衰减(weight decay)的由来。
那为什么权重衰减,让\(w\)减小可以减少过拟合?
(1)从模型的复杂度上解释:更小的权值w,从某种意义上说,表示网络的复杂度更低,对数据的拟合更好(这个法则也叫做奥卡姆剃刀),而在实际应用中,也验证了这一点,L2正则化的效果往往好于未经正则化的效果。
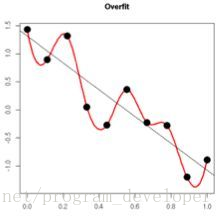
(2)从数学方面的解释:神经网络其实在拟合一种映射关系,找到一个函数,这个函数在所有训练数据上和真实值的偏差最小。比如在语义分割任务中,要把一张RGB图映射成分割图。再简单一些,我们把任务简化为一维空间,即输入x和输出y都是一维的,要找到一个函数\(y=ax^{n}+bx^{n-1}+cx^{n-1}+\cdots\)最能拟合所有样本\((x_i,y_i)\),函数中的x,y就是神经网络的输入(input)和输出(prediction),系数a,b就是神经网络的weights。但是最能拟合所有样本\((x_i,y_i)\)的函数就是最好的函数吗?我们评价一个网络的好坏不仅要看在训练集上的表现,也要看在测试集上的泛化性。所有训练样本\((x_i,y_i)\)肯定分布在二维空间的不同位置,如果一个函数真的能完全拟合上训练集样本上的所有点,那它一定是曲里拐弯的,如下图所示:
红线函数完全拟合了训练集样本空间上的所有点,但是它的泛化性很弱,它在测试集的性能可能还不如那条黑色的直线,所以红线函数并不是一个好的神经网络参数,所以为了提升网络的泛化性,其中一个可行的方法就是把曲里拐弯的函数拉直,让复杂的函数(网络)简单化。
那如何拉直呢?曲里拐弯的函数也就意味着它的变化很大,也就是说导数的绝对值很大,那我们让其导数值变小一些,它的变化是不是就没有那么剧烈了。回头看\(y=ax^{n}+bx^{n-1}+cx^{n-1}+\cdots\)这个神经网络的拟合函数,导数大小和a,b有直接关系,a,b就是神经网络的weights,也就是说让weights变小,就可以让拟合函数变得简单,让网络具有泛化性,那怎么让weights变小呢?加入l2正则化(之前已经讲过为什么了)!这样就实现了逻辑闭环:l2正则化->减少过拟合。
2. 那什么是weight decay?和l2正则化什么关系?
weight decay 是优化器层面的操作,直接体现在参数更新的规则中。Weight Decay 在优化器更新公式中,在计算梯度的时候加入网络的权重,作为新的梯度,即:
\[g_t =\eta\cdot g_t+\eta\cdot\lambda\theta\]
使用这个新的梯度在优化器内更新参数
\[\theta\leftarrow\theta-\eta\cdot g_t\]
也就是说,每次更新时,不只是用梯度,而且会把参数本身也拉小一点。
是不是和l2正则化很像?l2正则化是对于损失函数的修改,而weight decay是直接作用于优化器的参数更新步骤。两者都是为了让权重变小。
但是l2正则化有些情况下和weight decay相同,有些情况则不同
在SGD中,如果使用weight decay,其效果和l2正则化相同,也就是说,使用SGD和带有l2正则化的loss等同于使用带有weight decay的SGD和普通的loss。
但是呢,在Adam里,使用weight decay和l2正则化两者不等价,我们知道,weight decay的具体做法就是修改计算出来的梯度,在计算出来的梯度上加上网络参数的权重形成新的梯度,也就是修改\(g_t\),我们回顾Adam的公式(这里的公式我把\(s_t,v_t\)都代入了进去:
\[\theta_t\leftarrow \theta_{t-1}-\alpha\frac{\beta_1v_{t-1}+(1-\beta_1)(g_t+\boxed{\lambda \theta_{t-1}})}{\sqrt{\beta_2s_{t-1}+(1-\beta_2)(g_t+\lambda \theta_{t-1})^2}+\epsilon}\]
可以从上面的式子看出来,adam尽管引入了weight decay,对\(\theta_{t-1}\)的更新并不是像SGD、l2正则化一样,直接对参数减去\(\lambda \theta_{t-1}\),所以在adam里的weight decay不等于对损失函数进行正则化。除此之外,还有一个更棘手的问题,权重衰减的梯度是直接加在\(g_t\)上的,这就导致权重衰减的梯度也会随着\(g_t\)去除以分母。当梯度的平方和累积过大时,权重衰减的作用就会被大大削弱,会把\(\lambda \theta_{t-1}\)也做了自适应缩放,这也就是为什么Adam弱化了weight decay的作用。这就引出了AdamW,AdamW就是为了解决这个问题的。
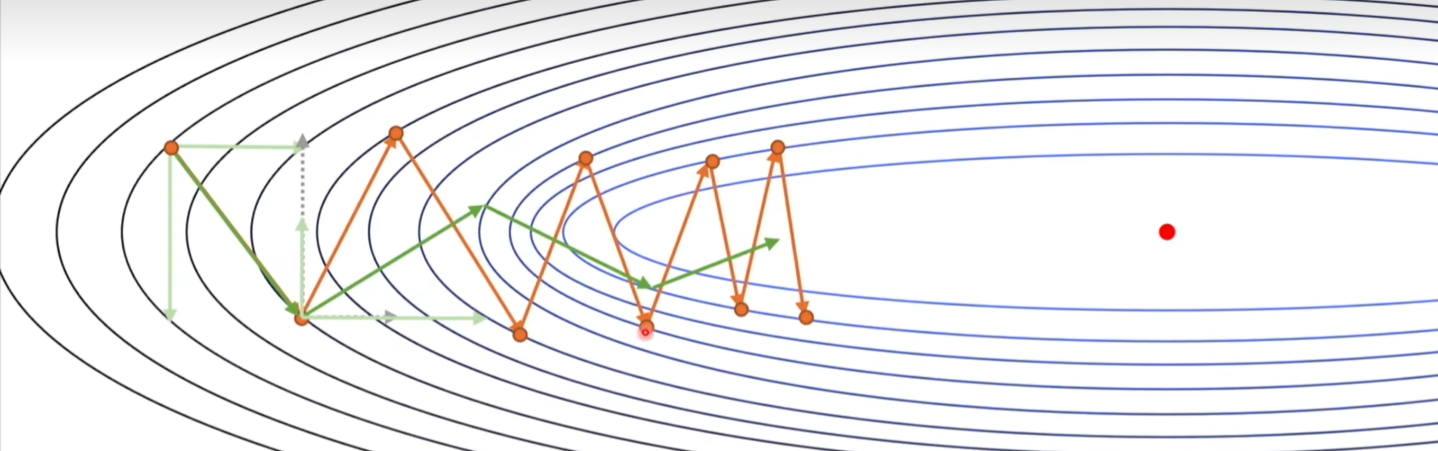
AdamW对这个问题的改进就是将权重衰减和Adam算法解耦,让权重衰减的梯度单独去更新参数,它不是把 weight decay 加入梯度中,而是 在参数更新外部“独立衰减参数”
如下图所示(注意绿色部分):

AdamW训练模型时,整体显存占用分析:
首先需要存储参数,然后还要存储一阶动量,就是梯度的指数移动平均,然后还要存储二阶动量,就是梯度的平方的指数移动平均,一阶和二阶就是Adam优化器所需要的参数。还有就是要存储梯度,与模型参数大小一致,所有任何优化器都需要梯度,梯度不由优化器管理,由框架自动管理。
还有一部分是,输入数据和中间激活值所占用的显存。
- 首先是输入数据部分,比如说RGB图像,[b, 3, 224, 224],单样本数据量为3*224*224 = 150528个元素,如果使用FP32,也就是4字节存储,假设b=128,占用内存为128 * 150528 * 4 / 1024 = 74MB,这部分占用,会在“数据加载→输入模型”时分配,前向传播开始后会被模型处理,通常不会长期占用(除非被缓存)。
- 然后是中间激活值部分,前向传播过程中产生的所有中间张量(如每层的输出、注意力 Q/K/V 矩阵、卷积层特征图等)。这是前向传播过程中产生的所有中间张量,是显存占用的核心来源,也是最容易被忽略的部分。为什么需要存储激活值?
推理时显存占用
首先就是模型参数占用的显存,这一部分和训练时没有差别,然后是中间激活值,要小于训练时的开销,推理时仍需存储中间激活值(用于前向传播的层间传递),但不需要保留到反向传播,因此部分框架会在计算后续层时自动释放已用过的激活值(“即时释放” 机制),显存峰值通常低于训练(训练需保留所有激活值供反向传播)。训练时需完整保留所有激活值供反向传播,而推理时可动态释放已使用的激活值,因此激活值的显存峰值更低(但仍可能是推理时的最大开销)。
训练时如果出现梯度消失问题怎么解决
- 使用残差连接
- 减少网络深度或者增加宽度
- 合适的权重初始化,避免初始权重过大或者过小,确保梯度在传播初期就处于“可传递”的范围
- 使用自适应学习率优化器,传统的SGD的学习率固定,若学习率很小,梯度更新很慢,如果过的大,可能会导致梯度爆炸。可以使用Adam,RMSProp,可以自适应更新每个参数的学习率
- 梯度裁剪:虽然这个方法是用于解决梯度爆炸问题,但也能间接缓解梯度消失,可以设定一个梯度阈值,超过阈值的梯度就缩小,避免因为某一层梯度爆炸二导致后续梯度被掩盖,就间接的让其他层的梯度失效了,表现为梯度消失
- 改进激活函数:传统的激活函数比如sigmoid,导数范围小,最大导数仅为0.25,容易传播时退化为0,可以使用ReLU及其变种.
- 使用Batch Normalization,比如sigmoid函数,当x很大(>5)或者很小的时候(<-5),其导数趋近于0,会导致梯度消失,通过BN,可以把输入“拉回”激活函数的非饱和区,让其回到有导数的区间内;同样,对于ReLU函数,即便在x>0时,梯度一直为1,但是如果遇到死亡ReLU的问题(即若某层 ReLU 的输入长期小于等于 0,该神经元的梯度会一直为 0),或者说,若深层网络的参数初始化不合理(如权重初始值过小),会导致前向传播时,每层的输入逐渐变小,最终被 “压到”x<0区间,BN会把输入拉到均值为0,方差为1的区间,并且可以通过仿射变换参数,让更多的输入落在>0的区间里,避免梯度消失
训练时Loss增大怎么办?
- 数据层面:训练数据中是否有坏样本?数据中是否有标签超出类别范围,或者有NaN或无穷大值,是否有归一化/标准化逻辑错误(如用错均值 / 标准差,或忘记处理新数据),导致输入数据分布突变。
- 模型层面:1)参数初始化不当,比如权重初始值过大(如全连接层权重初始化为 100),导致输入经过线性层后数值爆炸,反向传播时梯度失控。2)网络结构设计有问题,过深的网络导致梯度消失或者爆炸,引发loss一场
- 数值计算问题,看看是否存在除零、log(0)等操作?
- 训练层面:1)学习率太大,导致跳过最优解甚至发散,从合理参数瞬间跳到数值极大的参数。2)优化器选择不当,或者优化器的参数错误等等。3)加入梯度裁剪,当梯度爆炸的时候,对梯度进行截断,防止失控。4)加入权重衰减,防止模型数值快速增大,导致输出值异常。5)batchsize太小了,导致当前模型过拟合到当前batch,并且小batch梯度噪声大,导致梯度更新方向混乱。5)如果是测试集loss增大,有可能是模型过拟合到训练集了,可以加入早停、正则化、dropout等。
K-means算法
给定一堆无标签数据(比如一堆用户的消费数据、一堆图片的特征向量)和预设的聚类数量K,KMeans 要做的是:把数据分成K个簇(Cluster),让同一簇内的数据尽可能相似(簇内距离小),不同簇的数据尽可能不同(簇间距离大)。衡量 “相似性” 的核心指标是欧氏距离(默认,也可用曼哈顿距离等)—— 两个数据点的欧氏距离越小,相似度越高。
- 初始化:选择K个初始聚类中心
- 分配样本:给每个数据点分配中心,计算每个数据点到K个聚类中心的距离,然后把数据点分配到距离最近的中心所在的簇
- 更新聚类中心:对于每个簇,计算簇内所有数据点的均值,用这个均值作为新的聚类中心。
- 重复第二步和第三步,直到分类中心稳定:若所有数据点的 “所属簇” 都不再变化,或聚类中心的移动距离小于某个极小值(比如 0.001),就说明算法收敛,停止迭代。
缺点:
对于\(P(p_{1},p_{2},…,p_{n})\)和\(Q(q_1,q_2,…,q_n)\)、
欧氏距离:\(\mathrm{Euclidean}(P,Q)=\sqrt{\sum_{i=1}^n(p_i-q_i)^2}\)
曼哈顿距离:\(\mathrm{Manhattan}(P,Q)=\sum_{i=1}^n|p_i-q_i|\)
K-Means++
K-means++ 的核心就是优化初始聚类中心的选择逻辑,从 “盲选” 变成 “有策略的选”。
- 随机选择第一个初始中心
- 按照概率选择第2-k个初始中心:
- 假设已经选好了m个初始中心,现在要选第m+1个
- 对于每个数据点\(x\),计算其到m个中心的距离,取其中最小的那个距离,记为\(D(x)\)
- 将距离转化为概率:\(P(x)=\frac{D(x)^2}{\sum_\text{所有点}D(x)^2}\)
- 根据概率选择新中心,根据\(P(x)\)的分布,随机选择一个新的初始点作为第m+1个初始中心
- 重复2-4步,知道选出了k个初始中心
- 然后后续和传统的K-Means方法类似。
Dropout
Dropout通过在训练时随机“屏蔽”神经元,打破神经元之间的共适应,从而提升模型泛化能力,抑制过拟合。它相当于让一个神经网络,在训练时“每次都长得有点不一样”,迫使模型学出更稳健的特征。
- 打破神经元之间的依赖。在没有dropout的时候,不同神经元可能学会“协作”取记忆某些特定样本特征,dropout让这种协作不可靠,每个神经元必须学会更独立更鲁棒的特征
- 训练时相当于在训练很多不同的网络。每次dropout就是一个不同的子网络。测试时就相当于对这些网络取了一个平均,相当于集成学习的思想,多个模型平均结果泛化能力更强。
- 噪声的正则化效果。Dropout相当于引入了随机性,让模型更平滑,不对训练数据的噪声过于敏感。
如何解决模型陷入局部最优的问题?
- 使用更好的优化算法,比如优化器加入动量,让优化器冲出局部低估,自适应调整每个参数的学习率。
- 合理调整学习率,使用周期性学习率,让学习率时高时低,从坑里出来
- 使用Norm,稳定梯度分布,让优化空间更平整;加入Dropout,减少陷入局部末梢。
- 使用数据增强,增加数据多样性,让模型学习更稳健
- 改变模型结构,加入残差链接、skip connection,减少梯度消失,更改激活函数,使用ReLU等,避免使用sigmoid等
神经网络一般如何初始化?